Het Eötvös effect
Rond 1900 voerde een Duits team van het instituut voor geodesie in Potsdam zwaartekrachtmetingen uit aan boord van schepen die over de Atlantische, Indische en Stille oceaan aan het varen waren. Bij het bestuderen van de resultaten viel het de hongaars edelman en fysicus Lorand Eötvös op dat de metingen lager waren als de boot in oostelijke richting voer, en hoger bij beweging westwaarts. Hij herkende dat dit in de eerste plaats een consequentie was van het feit dat de Aarde om zijn as draait. In 1908 werden er nieuwe metingen uitgevoerd in de Zwarte zee op twee schepen, waarvan er één oostwaarts voer en één westwaarts. De resultaten bevestigden de bewering van Eötvös. Sinds die tijd gebruiken geodesisten de volgende formule om te corrigeren voor snelheid van het meetinstrument ten opzichte van de aarde.
De eerste term van deze formule correspondeert met het Eötvös effect, de tweede term correspondeert met een effect dat veel kleiner is dan het Eötvös effect.
| ar | corrrectie bij beweging ten opzichte van de Aarde |
| Ω | Draaing van de Aarde |
| u | Snelheid parallel aan breedtegraad (oost-west) |
| φ | breedtegraad waar de metingen worden verricht. |
| v | snelheid parallel aan lengtegraad (noord-zuid) |
| R | straal van de Aarde |
De fysische verklaring
Het Eötvös effect verandert hoeveel opwaartse kracht nodig is voor een voorwerp dat met zijn gewicht op de aarde rust.
Bij een luchtschip, ook wel bekend als zeppelin, is het zo dat het gewicht ervan feitelijk op de aarde rust, zowel wanneer het boven een vaste plek op de Aarde zweeft of wanneer het een snelheid heeft ten opzichte van de aarde.
Neem een luchtschip met een massa van tien ton (10,000 kilogram), met een kruissnelheid van 25 meter per seconde (90 km/h). Om uit te rekenen hoeveel drijfvermogen er geleverd moet worden tijdens stilstand van het luchtschip moet er rekening worden gehouden met de rotatie van de aarde. Een voorwerp dat zich op de evenaar bevind gaat al meebewegend met de aarde met een snelheid van 465 meter per seconde om de aardas heen. Bij de evenaar is de straal van de aarde 6378 kilometer. De hoeveelheid centripetale kracht die nodig is om met een snelheid van 465 meter per seconde langs een cirkel te bewegen met een straal van 6378 kilometer is 0.034 newton per kilogram massa. Voor een luchtschip van 10 ton is dat bij elkaar 340 newton. De hoeveelheid drijfvermogen die nodig is is de massa van het luchtschip (vermenigvuldigd met de zwaartekrachtversnelling), minus die 340 newton. Met andere woorden, een voorwerp dat op de evenaar met de aarde meebeweegt weegt 0,34 procent minder, dankzij de draaing van de aarde.
Wanneer het luchtschip met een snelheid ten opzichte van de aarde 25 m/s naar het oosten vliegt, dan is de snelheid van het luchtschip rondom de aardas 465 + 25 = 490 m/s, en daarvoor is een centripetale kracht van ongeveer 375 newton nodig. In westelijke richting vliegen met 25 m/s geeft een totale snelheid van 465 - 25 = 440 m/s, en daarvoor is ongeveer 305 newton nodig. Dus als een luchtschip eerst neutraal drijfvermogen heeft, en naar het oosten vliegt, en dan een U-bocht maakt, dan zal het gewicht van het luchtschip met 7 kilo toenemen; het drijfvermogen moet dan opnieuw worden afgeregeld. Op een niet om zijn as draaiende planeet zou dat verschil er niet zijn.
Een afleiding van de formule voor beweging langs de evenaar
Notatie:
| au | benodigde centripetale versnelling bij een snelheid u |
| as | benodigde centripetale versnelling bij stilstaan ten opzichte van de aarde. |
| Ω | Hoeksnelheid van de aarde: één omwendeling per siderische dag. |
| ωr | hoeksnelheid van een voorwerp ten opzichte van de hoeksnelheid van de aarde. |
| u | snelheid ten opzichte van de aarde. |
| R | straal van de aarde. |
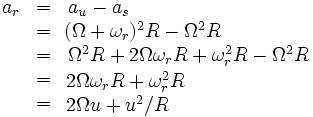
De algemene formule, hieronder herhaalt, simplificeert tot bovenstaande formule als de cosinus 1 is, en de factor v nul is.
Verklaring van de cosinus in de eerste term
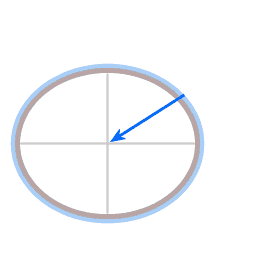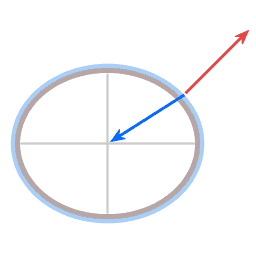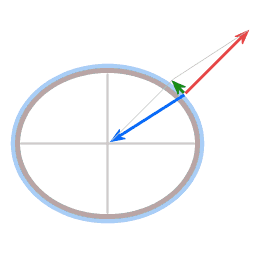
De zwaartekracht en de normaalkracht. De resultante kracht levert de benodigde centripetale kracht.
Omdat de aarde om zijn as draait is er een uitbuiking aan de evenaar. De zwaartekrachtwerking is gericht naar het middelpunt van de aarde. De richting van de normaalkracht is loodrecht op het plaatselijke oppervlak.
Op de polen en op de evenaar werken de zwaartekracht en de normaalkracht in precies tegenovergestelde richting. Op elke andere breedtegraad werken deze twee niet in precies tegenovergestelde richting waardoor er een resultante kracht is. Op iedere breedtegraad is er precies de hoeveelheid centripetale kracht die nodig is om een gelijkmatige dikte van de atmosfeer te handhaven. (De vaste Aarde is kneedbaar. Wanneer de vorm van de vaste Aarde niet in evenwicht zou zijn met zijn draaingssnelheid, dan zou schuifspanning in een tijdsbestek van miljoenen jaren schuifspanning de vaste aarde vervormen, totdat de schuifspanning is opgelost.)
Het voorbeeld van een luchtschip is opnieuw geschikt voor het bespreken van de krachten die er spelen. Wanneer het luchtschip een snelheid heeft ten opzichte van de Aarde, parallel aan een breedtegraad, dan is het gewicht van het luchtschip niet hetzelfde als wanneer het luchtschip boven een vaste plek zweeft. Als het luchtschip een snelheid heeft (ten opzichte van de Aarde) in oostelijke richting, dan gaat het luchtschip als het ware te snel. De situatie is dan te vergelijken met een raceauto op een circuit met afgeschuinde bochten. Als de raceauto te hard gaat voor die bocht (en er is niet genoeg grip) dan zal de auto naar de buitenkant van de bocht schuiven. Voor een luchtschip houdt dat in dat het gewicht verminderd vergeleken met de toestand van boven een vaste plek op de Aarde zweven. Als het luchtschip een snelheid in westelijke richting heeft is dat als die van een auto in een afgeschuinde bocht die te langzaam gaat, zonder grip zal de auto naar beneden glijden. For een luchtschip houdt dat een toename van het gewicht in.
Het Eötvös effect is evenredig met de component van de benodigde centripetale kracht die loodrecht staat op het plaatselijke oppervlak. Het Eötvös effect wordt beschreven met een cosinuswet: hoe dichter bij de evenaar, hoe sterker het effect.
Beweging langs 60 degrees noorderbreedte
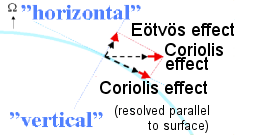
Het Eötvös effect voor een object dat oostwaarts beweegt langs 60 graden noorderbreedte. Er is een tendens om van de aardas vandaan te bewegen.
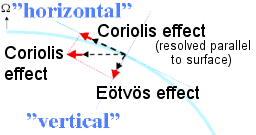
Het Eötvös effect voor een object dat oostwaarts beweegt langs 60 graden noorderbreedte. Er is een tendens om van de aardas vandaan te bewegen.
Een voorwerp dat zich op 60 graden noorderbreedte bevindt, mee-bewegend met de Aarde, beweegt langs een circlevormig traject, met een straal van ongeveer 3190 kilometer, en een snelheid van ongeveer 233 m/s.
Dat cirkelvormige traject vergt een centripetale kracht van ongeveer 0,017 newton foor iedere kilogram massa; 170 newton voor een luchtschip van 10.000 kilogram. Om het Eötvös effect voor 60 graden noorderbreedte uit te rekenen wordt de component die loodrecht staat op het plaatselijke oppervlak genomen, en op 60 graden noorderbreedte is dat de helft van de totale kracht. Hieruit volgt dat op 60 graden noorderbreedte het gewicht van een voorwerp dat met de Aarde meebeweegt 0,08 procent minder weegt, dankzij de draaiing van de Aarde.
Wanneer het luchtschip met een snelheid van 25 m/s oostwaarts vliegt wordt de totale snelheid 233 + 25 = 258 m/s, waarvoor een centripetale kracht van 208 newton nodig is, de plaatselijke vertikale component daarvan is 104 newton. Een snelheid van 25 m/s in westelijke richting wordt 233 - 25 = 208 m/s, waarvoor een centripetale kracht van 135 newton nodig is; verticale component 68 newton. Het verschil is zo'n 40 newton en het verschil tussen voor en na een U-bocht van een luchtschip van 10.000 kilogram (op 60 graden noorderbreedte) is dus een verschil van zo'n 4 kilogram in benodigd drijfvermogen.
De diagrammen tonen ook de component in de richting parallel aan het plaatselijke oppervlak. Het is in meteorologie en in oceanographie gebruikelijk om naar de effecten van de component parallel aan het plaatselijke oppervlak te verwijzen als het Coriolis effect.
Rotatie-vibratie koppeling
De voornaamste informatiebron voor dit artikel over het Eötvös effect is afkomstig van het volgende document:
The Coriolis effect PDF-file. 780 KB 17 bladzijden (engelstalig). Een algemene bespreking door de meteoroloog Anders Persson van verscheidene aspecten van geofysica. Onderwerpen: het Coriolis effect zoals dat in meteorologie en oceanografie in rekening wordt genomen, het Eötvös effect, de Slinger van Foucault, en Taylor kolommen.

Text, images and animations are licensed under a Creative Commons Attribution-ShareAlike 2.5 License.