Schijnbare beweging
De uitdrukking 'schijnbare beweging' wordt vaak gebruikt in de fysica. De uitdrukking wordt vaak bekritiseerd, want als het betekenisvol is om te spreken van 'schijnbare beweging', dan moet er ook een 'ware beweging' zijn, en hoe moet dat een betekenisvol onderscheid zijn?
De uitdrukking schijnbare beweging kan ondubbelzinnige betekenis gegeven worden door het te relateren aan het doel dat in de fysica op de eerste plaats komt: om de gebeurtenissen die plaatsvinden te verklaren in termen van de actie (of acties) van de fundamentele interacties van de Natuur: gravitationele interactie, Electromagnetische interactie, de zwakke nucleaire interactie en de sterke nucleaire interactie.
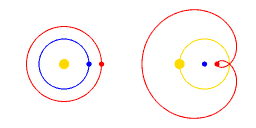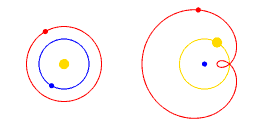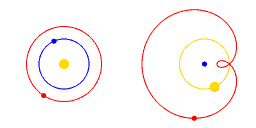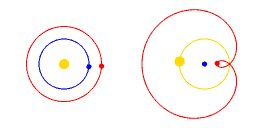
De gele cirkel stelt de Zon voor, de blauwe cirkel stelt de Aarde voor, en de rode cirkel stelt Mars voor.
Als de banen van de planeten en de andere objecten in het Zonnestelsel afgebeeld worden ten opzichte van een inertiëel coördinatensysteem dat meebeweegt met het massamiddelpunt van het zonnestelsel, dan kunnen de banen van alle hemellichamen verklaard worden in termen van zwaartekracht-interactie.
Aan de andere kant, als de banen van de planeten afgebeeld zijn in een coördinatensysteem dat zelf in versnelde beweging is ten opzichte van het massamiddelpunt van het zonnestelsel, dan wordt de beweging ten opzichte van dat coördinatenstelsel verklaart in termen van zwaartekracht-interactie, plus de coördinaat-versnelling die er speelt. De coördinaat-versnelling is de versnelling van het niet-inertiële coördinatensysteem ten opzichte van het inertiële coördinatensysteem.
In de animatie stelt de weergave aan de rechterkant de bewegingen van de Zon, Mars en de Aarde voor ten opzichte van een coördinatensysteem dat met de Aarde meebeweegt.
Een algemene eigenschap van coördinatentransformatie is dat onder coördinatentransformatie van het ene euclidische coördinatensysteem naar het andere alles behouden blijft. Alle relatieve posities blijven behouden, alle relatieve snelheden blijven behouden, alle relatieve versnellingen blijven behouden.
Bij het transformeren van de bewegingswetten naar een niet-inertiëel coördinatensysteem, blijven de bewegingswetten onveranderd. Het enige dat veranderd is de manier waarop de bewegingswetten worden genoteerd. Het transformeren van bewegingswetten naar een niet-inertiëel coördinatensysteem is vergelijkbaar met het transformeren van lengte-notatie van meters naar centimeters. In beide gevallen is er geen sprake van fysische inhoud.
Definitie van schijnbare beweging
Het volgende voorziet in een ondubbelzinnige definitie van 'schijnbare beweging':
Als een niet-inertiëel coördinatensysteem wordt gebruikt om beweging af te beelden, dan wordt er schijnbare beweging geïntroduceerd.
Definitie of inertiëel coördinatensysteem
De definitie van schijnbare beweging leunt volledig op het concept van inertiëel coördinatensysteem, dus dat moet scherp worden gedefiniëerd.
In de context van de bewegingswetten van Newton is het zo dat de bewegingswetten voorzien in een operationele definitie van het begrip 'inertiëel coördinatensysteem'.
Een coördinatensysteem is een inertiëel coördinatensysteem als het de volgende eigenschap heeft: Als beweging wordt afgebeeld in dat coördinatensysteem, dan komt naar voren dat Newton's bewegingswetten van toepassing zijn.
Er is in dit verband een interessante wederzijdse afhankelijkheid.
De relevantie van de equivalentie-klasse van inertiële coördinatensystemen werd aangevoeld voordat Newton's bewegingswetten werden geformuleerd. Galilei argumenteerde dat als we ons op een boot bevinden die met constante snelheid voortgaat, er voor een waarnemer in een afgesloten kamer op de boot geen experiment is dat hem in staat stelt om af te leiden wat de snelheid van de boot is.
Het herkennen van de equivalentie-klasse van inertiële coördinatensystemen maakte het mogelijk om het niveau van begrip te bereiken waarbij Newton's bewegingswetten konden worden geformuleerd.
Op het moment dat er een noodzaak wordt gevoeld om te voorzien in een operationele definitie van het begrip inertiëel coördinatensysteem blijkt dat de enige manier om dat te doen bestaat uit het aanroepen van Newton's bewegingswetten.
Dit illustreert dat het inherent onmogelijk is om een wetenschappelijke theorie te funderen op enkel fundamentele principes. Vergelijk electrische weerstand: R. De definitie van het begrip electrische weerstand is de wet van Ohm: R = V / I . Er is niet zoiets als eerst de de fysica van electrische weerstand definiëren en vervolgens de wet van Ohm ontdekken
In het boek 'Gravitation' van Misner, Thorne en Wheeler wordt deze kwestie ook besproken (paragraaf 12.3)
Point of principle: how can one write down the laws of gravity and properties of spacetime first (paragraph 12.1) and only afterward (here) come to grip with the nature of the coordinate system and its nonuniqueness? Answer: (a quotation from paragraph 3.2, slightly modified) "Here and elsewhere in science, as emphasized not least by Henri Poincaré, that view is out of date which used to say: 'define your terms before you proceed'. All the laws and theories of physics, including Newton's laws of gravity, have this deep and subtle character that they both define the concepts they use (here Galilean coordinates) and make statements about these concepts"
Samenvattend:
In de fysica, net als in alle menselijke inspanningen, is het doel van de theorieën het organiseren van de waarnemingen in overzichtelijke structuren. Het ondersteunend bewijs voor een theorie ligt in successen bij het toepassen van de theorie in de praktijk. Machines worden ontworpen, en als die machines werken zoals voorspeld is op basis van de theorie, dan ondersteunt dat de theorie.
De vier fundamentele interacties van de Natuur
Zoals gesteld in de openingsparagraaf: het doel dat in de fysica op de eerste plaats komt is om gebeurtenissen te verklaren in termen van de actie (of acties) van de fundamentele interacties van de Natuur: gravitationele interactie, electromagnetische interactie, zwakke nucleare interactie, sterke nucleaire interactie. Een visie op fysica die in conflict is met dat doel is een doodlopende weg.

Text, images and animations are licensed under a Creative Commons Attribution-ShareAlike 2.5 License.