Vergelijking van ballistische beweging en inertiaaloscillaties
Dit artikel leunt erop dat de lezer zich de inhoud van het voorgaande artikel eigen heeft gemaakt Inertiaaloscillaties
Ballistische beweging
Inertiaalbeweging ten opzichte van een inertiaal coördinatensysteem.

De blauwe stippen staan voor pucks die over een plat oppervlak glijden. ( De iets grotere stip vertegenwoordigt het afwerp mechanisme.
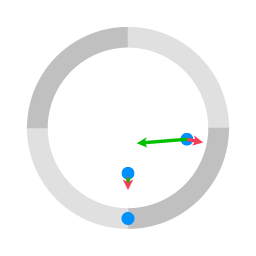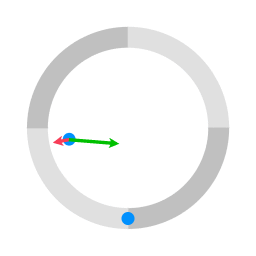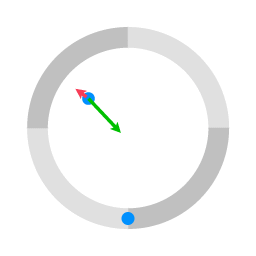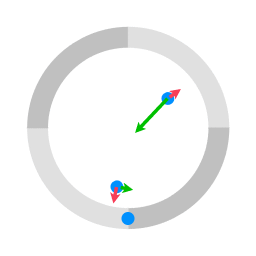
De groene pijlen staan voor de Coriolis term in de bewegingsvergelijking. De rode pijlen staan voor de centrifugale term.
De cirkel met vier kwadranten in animatie 1 staat voor een draaiend platform. De blauwe stippen staan voor voorwerpen die naar de andere kant worden geschoten, waarbij ze wrijvingsloos over het oppervlak glijden. De blauwe cirkel die met het platform meeroteert is de locatie van het afwerpmechanisme. Omdat er geen kracht is in een richting parallel aan het oppervlak bewegen de blauwe objecten langs een rechte lijn.
Beweging ten opzichte van een draaiend coördinatensysteem
In de bewegingsvergelijking voor beweging ten opzichte van een draaiend coördinatensysteem (in dit geval meedraaiend met het platform), worden de centrifugale term en de Coriolis term toegevoegd. In het geval van animatie 1 wordt er geen kracht op de pucks uitgeoefend (tenminste geen kracht in een richting parallel aan het oppervlak) dus de enige termen in de bewegingsvergelijking zijn de centrifugale term en de Coriolis term. De resultante vector van de centrifugale term en de coriolis term geeft de versnelling ten opzichte van het draaiende coördinatensysteem.
Een object in een baan rondom een perfecte bol

Wrijvingsloze beweging over het oppervlak van een perfecte bol. Het traject ten opzichte van het inertiaalsysteem is een grootcirkel. In deze animatie is er een hoek van 45 graden tussen het vlak van de grootcirkel en het vlak van de evenaar.
Neem in gedachte een satelliet in een baan om de Aarde op een constante hoogte ten opzichte van de Aarde, en neem als omlooptijd een sterredag. Wanneer vlak van die baan samenvalt met het vlak van de evenaar dan is de baan een geostationaire baan; de satelliet beweegt dan niet ten opzichte van de aarde. Maar als de baan gekanteld is ten opzichte van het vlak van de evenaar dan zal de satelliet niet stilstaan ten opzichte van de Aarde.
Animatie 3 toont de Aarde en het punt op de Aarde waar de sateliet recht boven staat. De satelliet zal de hele tijd van het noordelijk naar het zuidelijk halfrond oversteken en weer terug. Nog een aspect van de gekantelde baan is dat de satelliet niet boven dezelfde lengtegraad blijft hangen. Op de breedtegraden die het verst van de evenaar vandaan zijn zal de satelliet de Aarde als het ware "inhalen". Wanneer de satelliet het vlak van de evenaar passeert wordt de satelliet als het ware "door de Aarde ingehaald".
Animatie 3 kan ook worden opgevat als een weergave van het volgende gedachtenexperiment. Neem in gedachten een wrijvingsloze puck die rust op het oppervlak van een perfect bolvormige ijs-planeet. Zwaartekracht beperkt de beweging van de puck tot beweging parallel aan het oppervlak. Als je de puck een zet geeft, langs welk traject zal hij dan bewegen? En als de planeet onder de puck ronddraait, wat zal de beweging van de puck ten opzichte van de planeet dan zijn?
Om te beginnen, de draaing van de planeet onder de puck zal het traject ervan niet beinvloeden, het traject zal een grootcirkel zijn, met een uniforme hoeksnelheid ten opzichte van het middelpunt van de grootcirkel. Er is een nauwe analogie met het geval van beweging over een plat oppervlak zoals weergegeven in animatie 1. In bolgeometrie is een grootcirkel de tegenhanger van de rechte lijn van de geometrie van platte vlakken. In het geval van een perfecte bol werken de zwaartekracht en de normaalkracht in precies tegenovergestelde richting, waardoor er geen kracht in een richting parallel aan het oppervlak is.
Wanneer een kanon wordt afgevuurd zal het projectiel een Kepler-baan volgen, met het zwaartepunt van de Aarde in één focus van de baan. In het geval van een projectiel dat is afgevuurd door een kanon is de Kepler-baan zo klein dat het projectiel binnen enkele seconden zal inslaan op het oppervlak van de Aarde, maar de dynamiek van de baan staat daar los van. De lijn die het snijpunt vormt van het vlak van de Kepler-baan en het oppervlak van de Aarde is een grootcirkel. De lemniscaat (de figuur die lijkt op het cijfer 8) is het soort schijnbare afwijking dat je verwacht in het geval van een projectiel dat is afgebuurd vanaf het oppervlak van de Aarde.
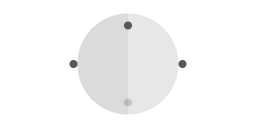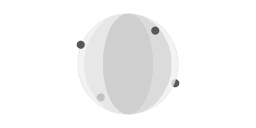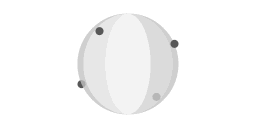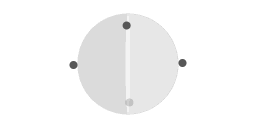
Wrijvingsloze beweging over het oppervlak van een perfecte bol. In deze animaties is de omloopperiode van de pucks twee keer zo lang als de omloopperiode van de bol.
Animatie 4 toont een weergave van het gedachtenexperiment van pucks die wrijvingsloos over het oppervlak van een perfecte bol glijden. De pucks doen er twee keer zo lang over om een volledige omloop te maken als de planeet, dus ze worden de hele tijd ingehaald door het oppervlak waar ze op rusten. In de omloopcyclus van de pucks is er telkens een punt waar de puck evenwijdig aan een breedtegraad beweegt. Een fase van evenwijdig aan een breedtegraad beweging wordt gevolgd door beweging richting de evenaar. De reden daarvoor is simpele geometrie: een grootcirkel die tangentiaal is aan twee breedtegraden (bv 30 graden noorderbreedte en 30 graden zuiderbreedte) blijft altijd binnen die twee breedtegraden.
Hetzelfde als wat voor de pucks geldt, geldt voor ieder projectiel dat in oost-naar-west richting wordt afgevuurd in langs een breedtegraad. Wat de snelheid van het projectiel ook is, omdat de lijn waarlangs het beweegt een grootcirkel is zal het projectiel na het afvuren voortgaan richting evenaar.
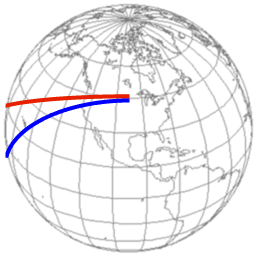
Verschil tussen draaiende bol en niet-draaiende bol
In het geval van de Aarde onder een afgevuurd projectiel: gezien vanaf de draaiende Aarde zal het projectiel een afwijking lijken te hebben van bewegen langs een grootcirkel. Op het noordelijk halfrond is deze schijnbare afwijking naar rechts.
In afbeelding 5 staat de blauwe lijn voor een grootcirkel die met de Aarde meebeweegt. De rode lijn staat voor de daadwerlijke beweging ten opzichte van de Aarde. Vergeleken met het niet-draaiende bol scenario zal het projectiel inslaan iets ten westen van de aanvankelijke vliegrichting (of in ieder geval rechts ervan).
Wat het niet-draaiend-bol en het draaiende-bol geval gemeenschappelijk hebben is dat als een projectiel in westelijke richting is afgevuurd het projectiel vervolgens richting de evenaar zal bewegen.
Inertiaaloscillaties
Beweging over het oppervlak van een parabolische schotel
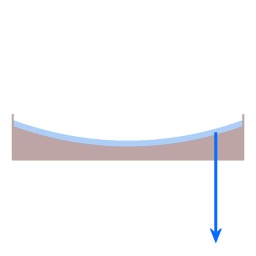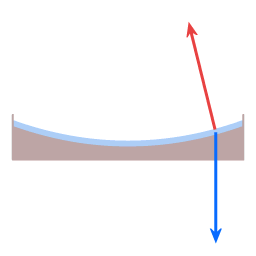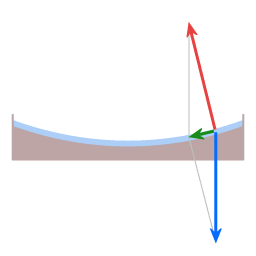
De rode pijl is de zwaartekracht. De groene pijl is de normaalkracht. De resultante kracht van levert de benodigde centripetale kracht. (De kromming van de schotel is sterk overdreven.)

Wrijvingsloze beweging over het oppervlak van een parabolische schotel
De linkerzijde van animatie 7 toont de beweging zoals gezien vanuit een niet-draaiend perspectief. De rechterkant toont de beweging zoals gezien vanuit een mee-draaiend gezichtspunt.
Afbuiging categoriseren
Het is hier van belang om een ondubbelzinnige definitie te hanteren van wat wordt gerekend als schijnbare afbuiging.
Als een "afbuiging" een artefact is van het afbeelden van beweging in een draaiend coördinatensysteem (of anderszins een versnellend coördinatensysteem), dan is het schijnbare afbuiging. Als een afbuiging wordt veroorzaakt door een kracht dan is ze onafhankelijk van wat voor coördinatensysteem wordt gebruikt om de beweging af te beelden. Bijvoorbeeld, de retrograde beweging van de planeet Mars is een schijnbare beweging, maar de baan van Mars rondom de Zon is dat niet.
Er is een oscillatie in de afstand van de puck tot het middelpunt van rotatie, en een oscillatie van de hoeksnelheid van de puck. Dat patroon van oscillaties wordt verklaard door arbeid die wordt verricht door een centripetale kracht, en dat patroon van oscillaties is hetzelfde wanneer de beweging wordt afgebeeld in een inertiaal coördinatensysteem en in een draaiend coördinatensysteem.
Beweging over het oppervlak van een afgeplatte sferoïde
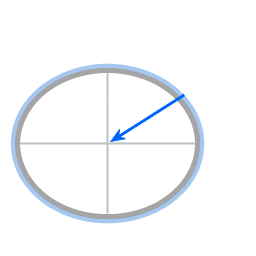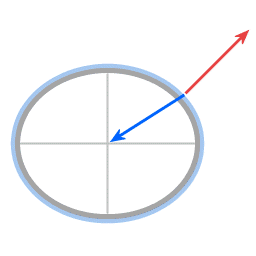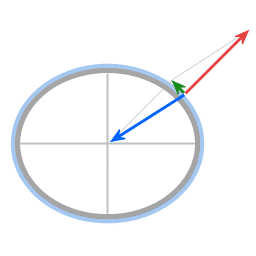
Krachten in het geval van een afgeplatte sferoïde
Rood: zwaartekracht
Groen: normaalkracht
De resultante kracht levert de benodigde centripetale kracht.

Inertiaaloscillatie over het oppervlak van een afgeplatte sferoïde.
Animatie 9 is een weergave van inertiaaloscillaties van een voorwerp dat in beweging is over het oppervlak van een ronddraaiende afgeplatte sferoïde.
Er is een verschil met de halve snelheid baan animatie die speciaal belangwekkend is. In animatie 9 is het voorwerp aan het oscilleren tussen "vooruit snellen" en "achterop raken" ten opzichte van de ronddraaiende beweging van de Aarde. Wanneer het voorwerp op zijn verst is vanaf de noordpool is zijn hoeksnelheid lager dan die van de Aarde, en dat komt overeen met in westelijke richting bewegen ten opzichte van de Aarde. Als gevolte daarvan trekt de poolwaartse kracht het voorwerp dichter naar de noordpool.
De halve snelheid baan animatie geeft een situatie weer waar geen poolwaartse kracht bij aan te pas komt. Zonder die poolwaartse kracht is het zo dat volgend op beweging in westelijke richting (ten opzichte van de Aarde) het voorwerp in de richting van de evenaar doorgaat. Dat is waar beweging zonder poolwaartse kracht en beweging met poolwaartse kracht letterlijk twee verschillende kanten uitgaan.
In het geval van ballistische beweging is er geen kracht die werkt in een richting parallel aan het oppervlak (Dat wil zeggen, in eerste benadering. Zie voor een meer gedetailleerde discussie zwaartekrachtpunt van het 'uitdijing aan de evenaar' artikel).
In het geval van een afgeplatte sferoïde is er een poolwaartse kracht, en in dat geval kunnen er inertiaaloscillaties zijn.

Text, images and animations are licensed under a Creative Commons Attribution-ShareAlike 2.5 License.