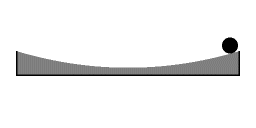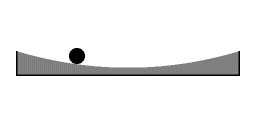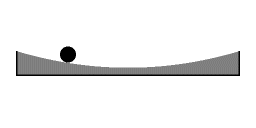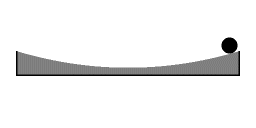
Inertial oscillations
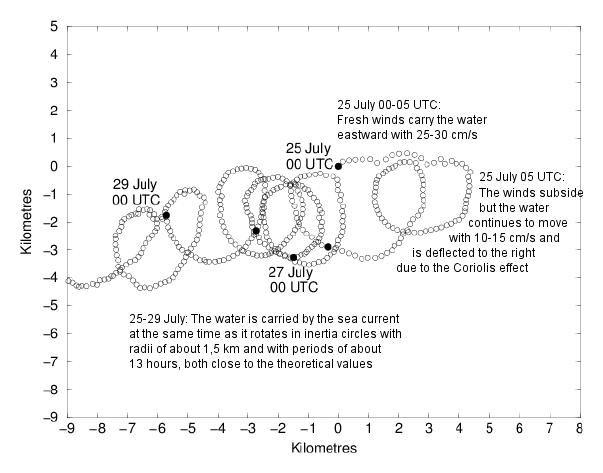
A drifting buoy set in motion by strong westerly winds in the Baltic Sea in July 1969. When the wind has decreased the uppermost water layers of the oceans tend to follow approximately inertia circles due to the Coriolis effect. This is reflected in the motions of drifting buoys. In the case there are steady ocean currents the trajectories will become cycloides.
The inertia circles are not eddies; a set of buoys close to each other would be co-moving, rather than revolve around each other
Rotating planet

Schematic representation of inertial oscillation.
The pattern of motion of the buoy that is being tracked is due to a pattern of dynamics that is present only in the case of a rotating planet. Animation 2 shows a preview. I will first discuss a simpler case, and then I will proceed to how it works for the Earth as a whole.
Also available: the java applet inertial oscillation, a 3D simulation of the physics of inertial oscillation.
Understanding of the physics of inertial oscillation is the key to understanding how the rotation of the Earth affects the oceanic and atmospheric dynamics. Inertial oscillation is the simplest, purest case. Usually the motion of air mass is affected by both pressure gradient and Coriolis effect. Inertial oscillation shows how water mass and air mass move when there is no pressure gradient to begin with, and no buildup of pressure gradient in the course of the motion.
Simpler case as physical model: parabolic dish
The dynamics of terrestrial inertial oscillations can be understood by noting the parallels with a simpler case: motion over the surface of a dish with a parabolic cross section.
In the fluid dynamics lab of the MIT Earth, Atmosphere and Planetary sciences faculty students can set up various demonstrations, and one of them is the construction of a parabolic turntable. A platform with a diameter of one meter, with a rim of a couple of centimeters, rotating at a constant angular velocity of about 30 revolutions per minute, is filled with a resin that takes several hours to set. Because the platform is rotating, the resin gets redistributed in such a way that in the final state the surface has a parabolic shape; the center is a centimeter or so deeper than the perimeter. The equilibrium state of the rotating fluid is called 'solid body rotation'. The formal name of the solid that is formed is 'paraboloid of revolution'. After the resin has set the surface is sanded to a smooth finish.
For demonstrations a small disk of dry ice is placed on the parabolic dish. The evaporating carbondioxide formes an air cushion, resulting in very low friction. Also, in demonstrations the parabolic dish must be rotating at exactly the same angular velocity as when it was manufactured.
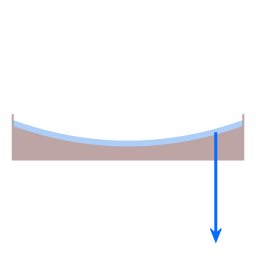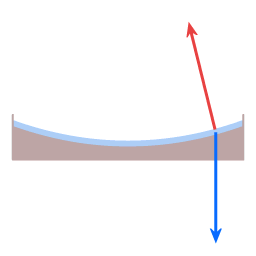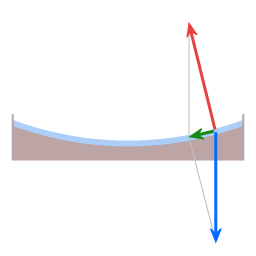
The blue arrow represents the force of gravity. The red arrow represents the normal force. The green arrow represents the resultant force.
When it was still liquid the resin was in solid body rotation, hence at every distance to the center of rotation the inclination of the surface is such that the resultant of gravity force and normal force provides the amount of centripetal force that is necessary to co-rotate with the dish.
If the puck is released in such a way that it has a small velocity relative to the dish then it will follow (to a first approximation) the trajectory that is shown on the left side of animation 4. The shape of the trajectory is an ellipse, and the motion is rather like an orbit. The right side depicts the motion as seen from a point of view that is co-rotating with the dish.
Frictionless motion along the surface of a parabolic dish. The arrow represents the centripetal force due to the inclination of the surface.
Orbit
Normally, the word 'orbit' is used for the motion of a satellite in space, being subject to the inverse square law of gravity. There are in fact two force laws that give rise to closed orbits. One is the inverse square law of gravity, and the other one is this case: a proportional force. The shallower the parabolic dish the better the validity of approximating the trajectories as ellipses. The MIT rotating dish demonstration shows a picture.
This motion allong an ellipse-shaped orbit can be thought of as a linear combination of two (perpendicular) harmonic oscillations. The following parametric equation of the position as a function of time describes the motion of the puck over the surface of the dish. The parametric equation provides a complete description: it describes the shape of the orbit and the velocity at each point in time.
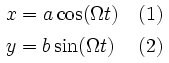
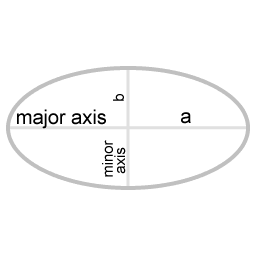
| a | half the length of the major axis |
| b | half the length of the minor axis |
| Ω | 360° divided by the duration of one revolution |
In the articles on this site I use the greek capital Ω (Omega) to refer to a constant factor; when the small greek letter ω (omega) is used it refers to the instantaneous angular velocity of some object. The instantaneous angular velocity of some object may fluctuate, depending on the circumstances. In the case of a harmonic force the trajectory of the object can be expressed as a function of a constant factor Ω.
Usually the orbit will be an eccentric orbit, and then the actual angular velocity oscillates, together with an oscillation in distance to the center of rotation.
Circle and epi-circle
Interestingly, the parametric equation can be rearranged into the following two components:
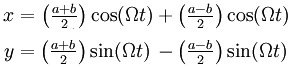
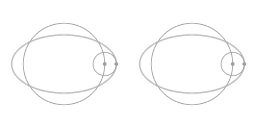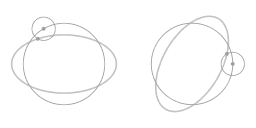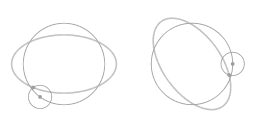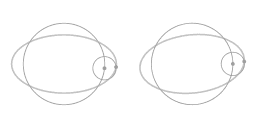
Animation 6 represents this rearrangement geometrically. It shows that the ellipse-shaped orbit has some remarkable symmetries: it can be thought of as a combination of two circular motions, both with uniform angular velocity Ω. The epi-circle corresponds with the degree of eccentricity of the overall orbit as compared to perfectly circular motion. When motion along this particular ellipse-shaped orbit is mapped in a rotating coordinate system the eccentricity of the ellipse-shaped trajectory shows up as motion along a small circle. In the case of modeling atmospheric dynamics on a parabolic dish this small circle is called an inertia circle.
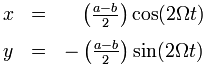
The factor 2 in the above parametric equation is especially noteworthy. The frequency of the motion along the inertia circle is twice the frequency of the overall rotation.
Separating the coordinate transformation
In this discussion I separate the task of taking coordinate transformation into account from the discussion of the physics. In this article, the coordinate transformations are taken care of by the animations, allowing me to focus on the physics taking place.
Java applet
When motion is mapped in a rotating coordinate system the rotation is taken into account by adding the centrifugal term and the coriolis term. The centrifugal term and the Coriolis term are depicted in the following interactive animation: Coriolis effect.
Careful arrangement
When the parabolic dish was manufactured the dish was rotating at a certain angular velocity, and the resin assumed a shape that matched the rotation rate. In other words, the manufacturing process tuned the parabolic dish to a certain rotation rate. The period of an orbit over the surface of that parabolic dish coincides with the dish's rotation rate. In demonstrations the instruction is to use precisely the same rate of rotation as when the parabolic dish was manufactured, and to use that angular velocity for the rotating coordinate system. The outcome of that careful arrangement is that the Coriolis term in the equation of motion matches the motion along the epi-circle precisely. This correspondence is visualized in the above mentioned interactive animation: Coriolis effect
Energy conversions: doing work
Harmonic oscillation; the restoring force is proportional to the distance to the center.
The case of inertial oscillation on a shallow parabolic dish and the rotational-vibrational coupling discussed in the previous article are perfectly analogous. In the case of inertial oscillations the potential energy reaches its maximum at the extremal points. As the object is being drawn closer to the center of rotation the centripetal force is doing work, converting potential energy to kinetic energy. The kinetic energy reaches its maximum at the points where the object is at its closest to the center of rotation. When the object moves away from the center of rotation again the centripetal force is doing negative work, decreasing the kinetic energy of the object.

Final situation after friction has dissipated the energy that was associated with the eccentricity of the trajectory.
Dissipation of energy
I will discuss dissipation of energy now, for that will reveal some interesting aspects. The natural process is: as long as a system can dissipate energy, it will. Consider a situation where the only way to dissipate energy is friction between the surface and the object that is supported by the surface. In the case of inertial oscillation there is dissipation of energy as long as there is a velocity with respect to the rotating parabolic dish. Friction reduces the eccentricity of the orbit. When the orbit has become circular there is still a lot of potential and kinetic energy, but as there is no friction there is no opportunity for energy dissipation.
Animation 8 depicts the state that the system will evolve to. Interestingly, it is an example of equipartition of energy. It is a common property of many kinds of dynamical systems that when the system has reached a final state (no more opportunity for energy dissipation) then the system's total energy will be divided evenly over the available degrees of freedom. Here, the available degrees of freedom are gravitational potential energy and rotational kinetic energy. The final state can be understood as energized degrees of freedom in a state of equilibrium with each other. In the final state the ratio of rotational kinetic energy to gravitational potential energy is 1:1 at every distance to the center of rotation. During manufacture of the parabolic dish, this is the state of equilibrium that the still liquid resin ended in when it reached a state of solid body rotation.
Analogy between parabolic dish and oblate spheroid

The blue arrow represents the force of gravity. The red arrow represents the normal force. The green arrow represents the resultant force.
Forces in the case of an oblate spheroid. The resultant force provides the required centripetal force.

Inertial oscillation over the surface of an oblate speroid.
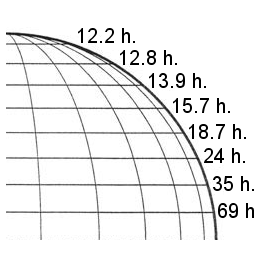
The theoretically predicted period of inertial oscillations at various latitudes.
The shape of the Earth and the shape of a parabolic dish manufactured as described above are analogous cases. The solid Earth is ductile; while the Earth's rock is brittle under impact, over periods of millions of years it behaves as a very viscous fluid. (For a demonstration of a very viscous fluid see the Pitch drop experiment.) The Earth's shape develops automatically towards an equilibrium shape. The equilibrium state is one of hydrostatic equilibrium. When the solar system was formed the Earth started out as a protoplanetary disk, and over time this distribution of space debris contracted and compacted to a final rotation rate and shape: an oblate spheroid. The current oblateness is tuned to the current rotation rate, just as the parabolic dish's manufacturing process tuned it to a particular rotation rate.
On the poles and on the equator the force of gravity and the normal force are exactly opposite in direction; on all other latitudes the two are not exactly opposite, giving rise to a resultant force, that provides the centripetal force that is necessary for buoyant objects to remain on the same latitude. Without this centripetal force objects would slide towards the equator.
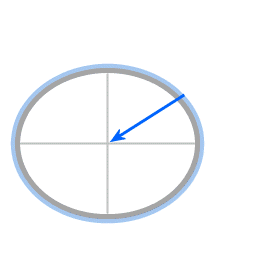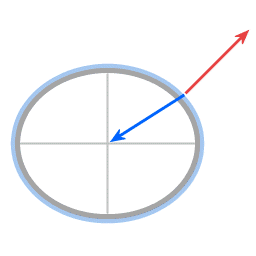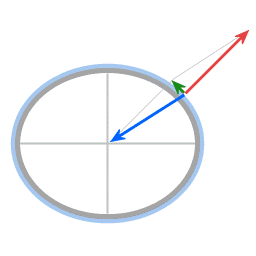
The centripetal force that is depicted in Image 10 can be decomposed in a component parallel to the local surface and a component perpendicular to the local surface. The component that is parallel to the local surface is called the poleward force.
Inertial oscillation over the surface of an oblate spheroid
In effect each hemisphere is a bowl, with the poles as points of lowest gravitational potential. Animation 11 represents the motion of a buoy that is co-moving with a mass of seawater that is in inertial oscillation as depicted in the image at the start of the article. The motion pattern is the same as the motion pattern depicted in animation 4. If you would be far in space, exactly above the north pole, but thousends of kilometers above it, then the ellipse-shape of the trajectory would be plain to see.
The depiction in animation 11 is highly schematized. Actual inertial oscillations of surface level seawater have amplitudes in the order of several kilometers, in the animation the oscillations have an amplitude that is a considerable fraction of the Earth's diameter.
As in the analogous case of motion over the surface of parabolic dish the motion pattern is determined by a centripetal force. There is an oscillation between the poleward force doing positive work and doing negative work. When the buoy is furthest away from the poles it is circumnavigating the Earth's axis slower than the Earth, and consequently the poleward force pulls it closer to the Earth's axis, and in pulling it closer the angular velocity of the buoy increases again.
There is a very interesting inertial oscillation visualizer available on the oceanmotion.org website. Try for example the following settings:
· Starting direction: Southward.
· Starting velocity 20 m/s.
· Latitude 15 degrees.
The Oceanmotion.org inertial oscillation visualizer also incorporates the beta-effect. Closer to the equator the Coriolis effect is weaker, so closer to the equator the deflection is less strong. As a consequence the inertion oscillation motion as a whole will travel westward.
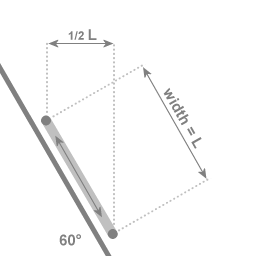
At 30 degrees latitude, when the inertial oscillation has an amplitude of L, the motion towards and away from the Earth's axis is 1/2 L
Dependency on latitude
The period of revolution of inertial oscillation is different at different latitudes. Diagram 12 shows the theoretically predicted period of inertial oscillation at various latitudes. The closer to the equator, the longer the period.
Work
Image 13 illustrates why the inertial oscillations have longer periods the further away from the poles. The amount of work that the centripetal force does is proportional to how much distance is travelled towards and away from the central axis of rotation. The inertial mass of the object in inertial oscillation is always the same, but the amount of work that the centripetal force does is not the same at every latitude; the closer to the equator, the smaller the amount of work that the centripetal force can do.
Buoyancy and the poleward force

The poleward force.
In Image 14 the small green arrow represents the poleward force. It's important to note that the poleward force applies if and only if the object is supported; it applies only when a normal force sustains the object's height with respect to the Earth's surface. Without the normal force (shown in red in the image) there is no poleward force.
An airship (also known as a zeppelin) is an interesting example of a buoyant object. It is tempting to think of an airship as weightless, having released itself from effects of gravity altogether, and accordingly it's tempting to expect an airship to move in the same way as a satellite does, only slower. In fact an airship is subject to a normal force, as the airship displaces a large volume of air. Gravity and the normal force do not act in exactly opposite direction, there is a small angle between them. Because of that small angle there is a resultant force, this resultant force provides required centripetal force. A satellite on the other hand is does not experience a normal force; a satellite is subject to gravity only.
To denote the sense of an object's weight being supported, with little to no friction to move parallel to the supporting surface, I use the expression 'buoyant'. All of the air mass of the atmosphere is buoyant, and hence subject to the poleward force.
In the next article Comparison of ballistics and inertial oscillations I discuss the contrast between inertial oscillation and ballistic trajectories.
Presence of other influences
Inertial oscillation is the case where any pressure gradient is negligably small, the only influence is the terrestrial Coriolis effect.
In the actual atmosphere pressure gradients are affecting the direction of air mass all the time. In the article formation of cyclonic flow. I discuss how the terrestrial Coriolis effect and pressure gradient force are both involved.
Why the oscillations are called inertial oscillations

Inertial oscillation over the surface of an oblate speroid.
Generally, inertial motion is asscociated with uniform motion along a straight line, and the motion depicted in the animation is far from uniform: it's not along a straight line and the velocity isn't constant. But there is another sense of 'inertial motion' that does apply in the case of inertial oscillation. In general, motion is referred to as 'inertial motion' when an accelerometer doesn't register any acceleration. Accelerometers onboard a satelite in orbit do not register acceleration since both the accelerometer casing and the movable parts inside are identically influenced by the Earth's gravitation. Orbital motion is free fall motion, the satellites are falling towards the Earth all the time - but they don't get there because they also have sufficient tangential velocity to overshoot the Earth all the time.
In the case of a buoy or a weather balloon that is moving along with inertial oscillation an onboard accelerometer would not register acceleration in the direction parallel to the local surface. Of course the accelerometer will register the gravitational acceleration that is associated with the local vertical component of the gravitational force; the buoy is supported by its buoyancy, the buoyancy support prevents it from "going with the flow" of the local vertical component of the gravitational acceleration. But the accelerometer won't register an acceleration parallel to the surface. The motion of the object parallel to the surface is motion that is "going with the flow" of gravitational acceleration, and then an accelerometer doesn't register acceleration. This illustrates again that it's useful to think of inertial oscillation as a form of orbital motion.
Comparison of ballistics and inertial oscillations.
Sources of information that were instrumental in developing this article:
- Persson, Anders 1998 How do we Understand the Coriolis Force? Bulletin of the American Meteorological Society 79, 1373-1385. (PDF-file, 374 KB)
- Persson, Anders The Coriolis effect - a conflict between common sense and mathematics PDF-file. 17 pages. A general discussion by Anders Persson of various aspects of the coriolis effect, including Foucault's Pendulum and Taylor columns. (PDF-file, 800 KB)
- Phillips, Norman., 2000 An Explication of the Coriolis Effect, Bulletin of the American Meteorological Society: Vol. 81, No. 2, pp. 299–303. (PDF, 200 KB)
(Also: available from a link provided by Thomas Reichler (University Utah) - Durran, D. R., 1993: Is the Coriolis force really responsible for the inertial oscillation?, Bull. Amer. Meteor. Soc., 74, 2179–2184; Corrigenda. Bulletin of the American Meteorological Society, 75, 261 (PDF-file, scans of magazine pages, 1.2 MB)
- Durran, D. R., and S. K. Domonkos, 1996: An apparatus for demonstrating the inertial oscillation, Bulletin of the American Meteorological Society, 77, 557–559. (PDF-file, scans of magazine pages, 1.3 MB)
Rigorous mathematical treatment of inertial oscillation:
- Ripa, Pedro 1996 ‘‘Inertial’’ Oscillations and the β-Plane Approximation(s) Journal of Physical Oceanography, Volume 27, Issue 5, pp. 633–647, (PDF-file, 290 KB)
History of understanding of the Trade Winds:
- Persson, Anders Hadley’s Principle: Understanding and Misunderstanding the Trade Winds. (PDF-file, 244 KB)

This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.