Cet article est une introduction réduite à l'essentiel. Il n'y a pas ici de mathématiques, mais beaucoup de schémas et d'animations. Les autres articles de ce site ont le contenu mathématique permettant de démontrer les déclarations qui y sont faites. Ici, vous aurez à me croire sur parole.

La force de Coriolis en météorologie

Sur cette page, je discute de l'effet de la rotation de la terre pris en compte en météorologie. On appelle cet effet «force de Coriolis». (Pour l'effet de la rotation de la terre qui s'applique en balistique, voir les deux simulations Java: Les grands cercles et balistique).

La première conséquence du fait que la terre est en rotation est que ce n'est pas une sphère parfaite ; il y a un renflement équatorial. La terre a été moulée de la même forme qu'une planète complètement liquide aurait pu l'être. Le renflement est faible ; sur les images de la terre prises de l'espace, vous ne le voyez pas, et il peut donc sembler négligeable, mais il n'en est rien : ce qui importe en météorologie est un effet provoqué par la rotation de la terre combiné avec l'aplatissement qui en résulte.

Un modèle: l'assiette parabolique

Représenter le mouvement sur la surface de la terre est assez compliqué ; je me tournerai donc vers un modèle plus simple, mais qui présente les caractéristiques donnant lieu à l'effet de la force de Coriolis.

Source: PAOC, MIT  Courtesy of John Marshall

L'assiette visible sur la photo est un peu plus profonde au centre qu'à l'extérieur. Elle a été fabriquée comme suit : un cylindre plat, muni d'un bord, tourne à une vitesse angulaire constante (précisément 10 tours par minute), et une résine de synthèse a été répandue sur ce plateau. La résine, liquide, s'est répartie elle-même en couvrant toute la zone. Elle a eu assez de temps pour atteindre un état d'équilibre avant de commencer à se solidifier. L'état final est un équilibre entre la tendance à s'écouler en poussant vers l'extérieur et en remontant vers le bord, et la tendance de la force de gravité à rendre la surface du fluide totalement plane. Une fois dure, la surface a été poncée pour obtenir une finition très lisse. La section transversale de la surface concave est une parabole. En raison du manque de profondeur, il est difficile de le voir, mais il s'agit en fait bien d'une parabole.

Notez également la construction suspendue au-dessus de la parabole. La barre verticale n'est pas attachée à la table supportant le plateau, mais à ce plateau lui-même ; quand l'assiette tourne, cette barre tourne avec elle. La construction en surplomb comporte une caméra vidéo, donc les images de cette caméra montrent le mouvement vu en co-rotation avec l'assiette.

On peut démontrer mathématiquement que la section diamétrale de la surface obtenue est une parabole. Voici comment cette assiette parabolique sert de modèle pour la terre en rotation : si vous versez de l'eau sur l'assiette (pendant qu'elle est en rotation à la même vitesse de 10 tours par minute), la distribution de cette eau se passe de la même façon que celle de la résine au moment de sa répartition. L'eau aura donc partout une épaisseur uniforme.

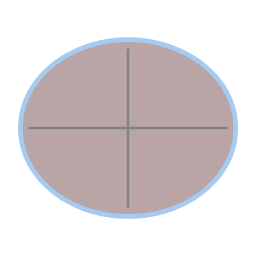
La forme naturelle d'une surface d'eau est plate. En raison de la rotation, la surface de l'eau prend une forme parabolique.

La forme naturelle d'une planète est sphérique. En raison de sa rotation, la terre prend une forme aplatie, avec l'eau de la planète comme une couche de quelques kilomètres d'épaisseur en surface. Par ailleurs, la terre n'a pas obtenu sa forme aplatie actuelle à partir d'une forme sphérique. Au début de la vie de notre système solaire, quand la terre a commencé à se former, elle avait la forme d'un disque protoplanétaire. En vertu de son auto-gravité, ce disque protoplanétaire s'est contracté de plus en plus en une planète. En raison de la rotation, la contraction n'a pas eu lieu jusqu'à aboutir à une forme sphérique.

L'assiette parabolique est creuse, concave, et la terre est convexe. Il n'est donc pas simple de reconnaitre une assiette parabolique comme modèle de la terre. La série suivante de quatre images a été conçue pour résoudre ce dilemme.

A

B

C

D

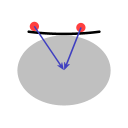
L'image A montre que si une assiette grande comme un continent était posée sur le pôle nord, la force de gravité de la terre aurait tendance à tirer les objets de l'assiette vers le milieu.

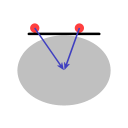
Dans l'image B, la ligne droite représente un énorme disque parfaitement plat. Même si ce disque est plat, le fait que la gravité de la terre tire vers le centre de la terre, tous les objets posés sur le disque ont tendance à aller au milieu.

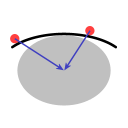
Dans l'image C, la ligne représente une surface qui a en commun avec les deux exemples précédents que les objets situés sur elle auront tendance à aller au milieu. Même si cette surface est convexe, c'est effectivement une cuvette — du point de vue d'un Terrien — parce que l'extérieur, le bord de la surface, est plus éloigné du centre de gravité de la terre que le milieu.

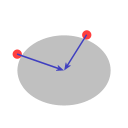
Enfin, l'image D représente la situation sur terre, avec son renflement équatorial. En effet,chaque hémisphère est une cuvette, et l'équateur est le rebord de ces deux cuvettes.

Force

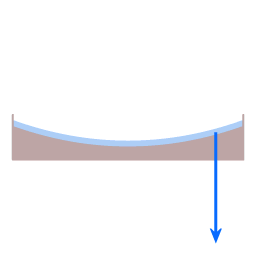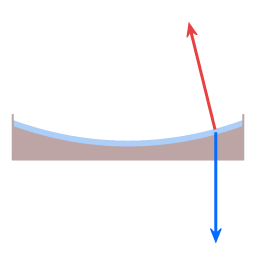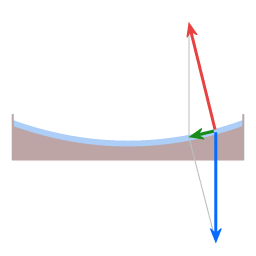
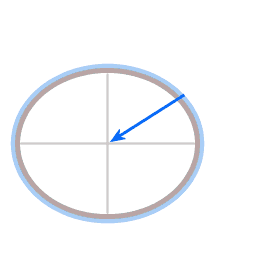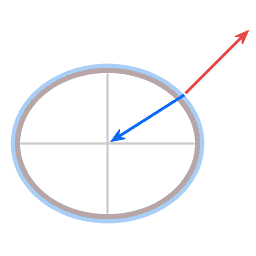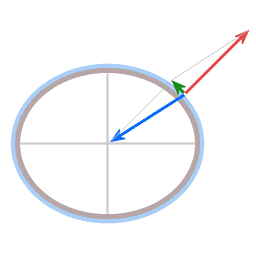
Sur les deux schémas, la flèche bleue représente la force de gravité. Dans le cas du plateau, elle est dirigée verticalement vers le bas ; dans celui de la planète, elle tire vers le centre de la terre. La flèche rouge représente ce que l'on appelle «la force normale». (Ici, le mot «normal» est utilisé dans son sens mathématique, c'est à dire perpendiculaire). La surface de l'assiette porte l'eau qu'elle contient, ce qui signifie que la surface exerce une force sur l'eau, exactement perpendiculaire à la surface.
Le plus souvent, la gravité agit également perpendiculairement à la surface, ce qui entraîne un équilibre statique, donc en général la force normale et la gravité s'annulent. Mais dans les cas ci-dessus, la force normale et la gravité ne sont pas exactement dans la direction opposée.

(Pour les remarques sur la taille du renflement équatorial de la terre, et la mesure de la force intérieure, voir la discussion du Renflement Equatorial ci-dessous.)

Glissement sur l'assiette parabolique.

On ne verse pas de l'eau sur cette assiette, ce qui la rendrait trop lourde. Au lieu de cela, pour les démonstrations, de petits objets fabriqués pour avoir très peu de friction sont placés sur sa surface.

Dans l'animation ci-dessus deux points de vue sont présentés côte à côte. À gauche, le mouvement réel de la boîte, à droite, le mouvement vu de la caméra en surplomb (qui tourne avec l'assiette). Sur le bord du disque, deux nuances de gris divisent le bord en quatre quadrants, pour voir clairement laquelle des deux vues est en rotation.

L'objet sans friction a été placé sur l'assiette parabolique de manière qu'il est tout simplement en co-rotation avec l'assiette. L'assiette est en rotation avec la même vitesse angulaire que quand elle a été fabriquée. Dans ce cas, la force centripète (vers l'intérieur) résultant de la pente est précisément la valeur nécessaire pour soutenir le mouvement le long d'un cercle. Si vous placez plusieurs objets sur l'assiette en rotation, tous avec une vitesse nulle par rapport à l'assiette, alors ils garderont chacun tout simplement leur position par rapport aux autres objets. Dans ce cas, si vous avez seulement l'image de la caméra surplombante, vous aurez du mal à dire si vous êtes en train de regarder un ensemble tournant ou un ensemble fixe.

Toutefois, lorsque l'objet a une certaine vitesse par rapport à l'assiette en rotation, des choses intéressantes se produisent.

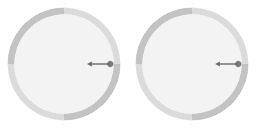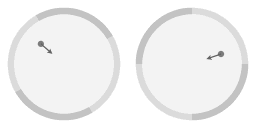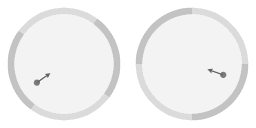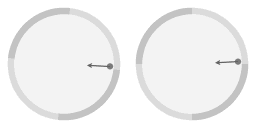
Dans l'animation ci-dessus, une flèche a été ajoutée pour mettre en évidence que la pente de la surface donne lieu à une force centripète (tournée vers l'intérieur). Près du bord, la force centripète est plus forte parce que le pente est plus raide. En fait, elle est proportionnelle à sa distance au centre : une propriété de la forme parabolique est que la force centripète qui résulte de la pente est exactement proportionnelle à la distance de l'axe central de rotation. A partir de là, nous écrirons «force proportionnelle» comme raccourci pour désigner «une force qui est proportionnelle à la distance de l'axe central de rotation».

Par rapport au mouvement circulaire, l'objet sans friction a été légèrement poussé ; on lui a donné une certaine vitesse par rapport à l'assiette parabolique. Cependant, en moyenne, l'objet est toujours en co-rotation avec l'assiette, c'est juste que sa trajectoire n'est plus circulaire, mais en forme d'ellipse.

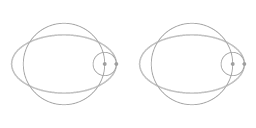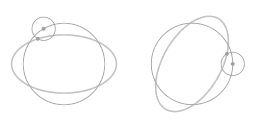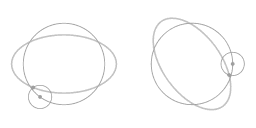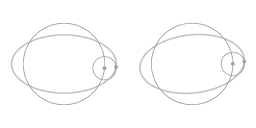
L'animation ci-dessus montre que le mouvement le long de la trajectoire elliptique peut être considérée comme une combinaison de deux cercles : un cercle principal et un épi-cercle. À partir d'une vue en co-rotation, ce que vous voyez est précisément le mouvement le long de l'épi-cercle.

Règle du mouvement

L'assertion suivante est démontrée dans d'autres articles de ce site ; je vais simplement énoncer ici cette règle du mouvement :

• Lorsque la force provoquant le mouvement circulaire est proportionnelle, alors le mouvement apparaissant d'un point de vue en co-rotation est précisément l'épi-cercle.

Voici ce qui est important pour la règle du mouvement :

• Pendant qu'un objet se déplace le long de l'épi-cercle, il est constamment en train de tourner (et dans les exemples montrés ici la rotation se fait vers la droite). Le fait que l'épi-cercle soit effectivement un cercle parfait signifie que la tendance à tourner vers la droite a la même force dans toutes les directions.

Cette règle du mouvement s'applique à la fois dans le cas du mouvement sur la surface de la parabole et dans le cas du mouvement sur la surface de la terre.

Cause de la rotation

La cause de la rotation est différente dans chaque direction, mais le facteur commun est que dans toutes les directions c'est une interaction entre la force centripète et l'inertie de l'objet en rotation.

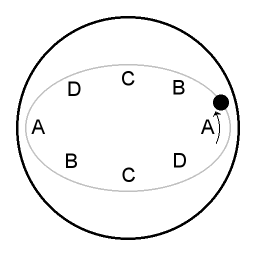
En détail : A   Lorsque l'objet mobile est au niveau des points A de la trajectoire il tourne plus lentement que l'assiette parabolique elle-même. La rotation est plus lente en raison d'un excès de force centripète, et l'objet est donc tiré plus près de l'axe central. C   Lorsque l'objet est au niveau des points C de la trajectoire il tourne plus rapidement que l'assiette parabolique elle-même. Il n'y a alors pas suffisamment de force centripète, et donc l'objet s'éloigne à nouveau de l'axe central. B   Aux points B de la trajectoire, l'attraction centripète augmente, et l'objet gagne de la vitesse. D   Aux points D, l'objet est en mouvement contre l'attraction de la force centripète, et en conséquence il perd de la vitesse.

A	Lorsque l'objet mobile est au niveau des points A de la trajectoire il tourne plus lentement que l'assiette parabolique elle-même. La rotation est plus lente en raison d'un excès de force centripète, et l'objet est donc tiré plus près de l'axe central.
C	Lorsque l'objet est au niveau des points C de la trajectoire il tourne plus rapidement que l'assiette parabolique elle-même. Il n'y a alorspas suffisamment de force centripète, et donc l'objet s'éloigne à nouveau de l'axe central.
B	Aux points B de la trajectoire, l'attraction centripète augmente, et l'objet gagne de la vitesse.
D	Aux points D, l'objet est en mouvement contre l'attraction de la force centripète, et en conséquence il perd de la vitesse.

(On peut se demander si la rotation peut aussi être expliquée par un exemple qui utilise le déplacement en ligne droite. Pour une réponse voir la discussion ligne droite dans le paragraphe Remarques ci-dessous.)

Ajout d'un gradient de pression à l'image

La leçon à tirer du mouvement sur la surface de l'assiette parabolique peut maintenant être appliquée au mouvement à la surface de la terre : la tendance à dévier est aussi forte dans toutes les directions.

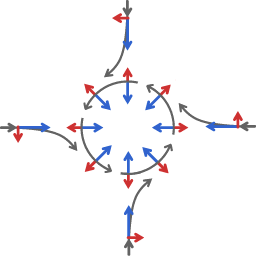
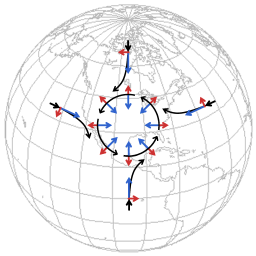
En météorologie, les deux principaux facteurs affectant le mouvement des vents sont la force du gradient de pression et celle de la force de Coriolis. Les images suivantes représentent la formation de l'écoulement autour d'une zone de basse pression.

Les flèches bleues représentent la tendance à l'écoulement vers une zone de basse pression, les flèches rouges représentent la force de Coriolis. Les diagrammes sont très schématiques, pour en faire ressortir les caractéristiques essentielles.

Au début, les masses d'air soumises au gradient de pression commencent à s'écouler de tous les côtés vers la zone de basse pression. Tous les flux, à partir du nord, du sud, de l'est ou de l'ouest dévient vers la droite de leur direction initiale. Le résultat global de la déviation est que les flux se guident les uns les autres dans un modèle d'écoulement autour de la zone de basse pression. À la fin, le sens d'écoulement devient perpendiculaire au gradient de pression.

Le flux autour de la zone de basse pression se caractérise par une sorte de lutte féroce entre le gradient de pression et la force de Coriolis.

Et il y a un autre cas où la force de Coriolis demeure un facteur actif : lorsque l'ensemble des champ d'écoulement se contractent, il y a une composante centripète de la vitesse. Chaque fois qu'une composante centripète de vitesse apparaît, la force de Coriolis dévie cette composante de vitesse en un flux d'écoulement qui est une fois de plus perpendiculaire au gradient de pression. Ainsi, la force de Coriolis ne favorise pas seulement la formation d'un écoulement autour de la zone de basse pression, mais il soutient également cet écoulement.

Points clefs

• Dans la physique des mouvements de l'atmosphère, à la plus grande échelle, l'influence principale est la force qui soutient le mouvement de rotation. Toutes les masses d'air sont à tout moment soumises à une force en direction de l'axe de la terre.
• En raison de cette force, les masses d'air qui n'ont pas de vitesse par rapport à la rotation de la terre restent en co-mouvement avec celle-ci, et la direction des masses d'air qui ont une vitesse relative à la terre est déviée.
• La tendance à changer de direction (par rapport à la terre) est la même dans toutes les directions.

Remarques

Renflement équatorial

A l'équateur, la surface de la terre est d'environ 20 km plus loin du centre géométrique de la terre qu'aux pôles. Par rapport au rayon total de la terre de 6400 kilomètres cela peut sembler une très petite différence, et l'on pourrait être tenté de penser que ce renflement est négligeable.

Dans notre illustration, l'angle entre la flèche rouge et la flèche bleue est exagéré pour plus de clarté ; dans le cas de la terre réelle, cet angle, à une latitude de 45 degrés, est d'environ un dixième de degré. Cette pente descendante de 0,1 degré fournit la force centripète nécessaire vers l'intérieur.

À raison d'une révolution par jour, quelle force centripète est nécessaire pour faire le tour de l'axe de la terre ? Pour la latitude de 45 degrés le calcul donne, pour un objet ayant une masse de 1 kilogramme, qu'une force de 1,7 gramme-force est nécessaire. Le rapport est de 1/580. Donc, quelle que soit la mesure de poids que vous utilisez, divisez par 580 et vous aurez la force centripète nécessaire.

(Au cas où vous décidiez de vérifier le nombre que je présente ici : la force centripète nécessaire que j'ai donnée est la composante parallèle à la surface locale, comme le montre le diagramme.)

Je pèse environ 80 kg, et pour moi la force nécessaire est donc d'environ 140 gramme-force. Si vous avez une balance à portée de main, appuyez dessus en exerçant une force de 140 grammes pour vous faire une idée.

Explication pour un mouvement en ligne droite ?

Ici, j'examine si la déviation qui est si typique de l'effet de la rotation de la terre peut également être expliquée par un exemple basé sur le mouvement en ligne droite. Pour ce faire, je vais examiner deux cas, l'un avec un mouvement sur l'assiette parabolique, et l'autre avec un mouvement sur une surface plane. Je vais invoquer la phrase suivante comme critère essentiel : l'effet de la rotation de la terre qui est en jeu dans l'atmosphère est le même pour toutes les directions du mouvement.

Patinoire parabolique

Imaginez que vous êtes sur une patinoire parabolique. Il faudrait pour cela une très grande plate-forme. Il y a en France un centre scientifique qui a un réservoir en rotation de 13 m de diamètre. Lorsque cette masse d'eau en rotation est dans un état d'équilibre, vous pourriez essayer de la congeler, ce qui formerait une patinoire parabolique.)

Imaginez que vous êtes sur cette patinoire, en co-rotation avec elle (et la patinoire est en rotation avec la même vitesse angulaire que quand elle a été fabriquée). Vous donnez à une rondelle de hockey sur glace un coup de pouce dans le sens de la rotation de la patinoire pour qu'elle se mette en marche. En la poussant, elle tournera toujours autour de l'axe central, mais de façon plus rapide que la patinoire elle-même. La rondelle va alors commencer à s'éloigner de l'axe central.
Ensuite, donnez à la rondelle de hockey sur glace une poussée vers l'arrière : elle fait alors le tour plus lentement que la patinoire elle-même, et elle commence à s'affaisser vers le centre.

Disque plat

Maintenant, faisons la même expérience sur la surface d'un disque plat en rotation. L'animation ci-dessous illustre une telle configuration. Vous voyez plusieurs rondelles en cours de lancement dans le même temps, se déplaçant toutes le long de la même ligne droite, mais avec des vitesses différentes.

Les rondelles qui se déplacent vers l'avant s'éloignent de l'axe central. OK, c'est un peu la même chose que dans le cas parabolique

Que diriez-vous de la rondelle qui se déplace vers l'arrière ? Les rondelles en mouvement arrière sont en recul par rapport à l'axe central de rotation aussi ! Elles s'éloignent car elles se déplacent le long d'une ligne droite qui est tangente à la plate-forme circulaire. Ainsi, sur un disque plat, il n'y a pas de différence si les rondelles vont vers l'avant ou l'arrière : de toute façon elles s'éloignent de l'axe central de rotation.

La réponse à la question est Non : en météorologie la déviation du mouvement à l'égard du système en rotation ne peut pas être expliquée par un exemple basé sur le mouvement en ligne droite.

D'autres documents sur ce site

La suite de la discussion sur la force de Coriolis terrestres est dans l'article Oceanographie: Oscillations Inertielles

La suite de la discussion sur la force de Coriolis terrestres est dans l'article Oceanographie: Oscillations Inertielles

Applications Java

Applicable en Météorologie :

• La Simulation des Oscillations Inertielles

Applicable en Balistique :

• La Simulation des Grands Cercles. Comme son nom l'indique, cette simulation montre le mouvement le long d'un grand cercle à la surface d'une sphère. La simulation montre en même temps à quoi ça ressemble d'un point de vue fixe et d'un point de vue en co-rotation.
• La Simulation balistique et des orbites Avec cette simulation, vous pouvez lancer un projectile de n'importe où sur la planète, dans n'importe quelle direction, la simulation calcule alors la trajectoire.

Traduit en français par Damien Belliard et François de Dardel

Texte, images et animations sont placé sous licence : Creative Commons Attribution-ShareAlike 2.5 License.