De algemene theorie van relativiteit

De presentatie in dit artikel van de algemene theorie van relativiteit volgt niet de historische ontwikkeling, al worden wel vele historische gebeurtenissen besproken.

In dit artikel wordt de newtoniaanse dynamica zo gepresenteerd dat de overgang naar relativistische dynamica zoveel mogelijk wordt voorbereid.

Dit artikel gaat ervan uit dat de lezer op zijn gemak is met de inhoud van het voorafgaande artikel over speciale relativiteit.

Voorbereiding: Newtoniaanse dynamica

Velden

In de loop van de 19de eeuw werd het gebruikelijk om de wetmatigheden van de beweging van deeltjes in termen van velden te begrijpen. Deeltjes zoals een electrisch geladen deeltje werden voorgesteld als de bron van een veld, en andere deeltjes kunnen dan een interactie hebben met dat veld. In plaats van te veronderstellen dat deeltjes direct een kracht op elkaar uitoefenen wordt de aanwezigheid van een veld verondersteld, en dat veld treedt dan op als overbrenger van de interactie.

Newton had als eerste ingezien dat als de wetmatigheid van behoud van impuls grote implicaties heeft. Het zonnestelsel was naar mocht worden aangenomen stabiel. Newton zag in dat als impulsmoment van de planeten van het zonnestelsel niet behouden zou zijn het zonnestelsel niet op langere termijn stabiel zou zijn, en impulsmoment is alleen behouden in het geval van een instantaan werkende zwaartekracht. De evidente stabiliteit van het zonnestelsel maakte de newtoniaanse aanname van instantaan werkende zwaartekracht onvermijdelijk. Dat is de achtergrond van de newtoniaanse aanname dat zwaartekracht een instantane actie-op-afstand is.

In de loop van de 19e eeuw werd het duidelijk dat een verandering van de bron van een electromagnetisch veld zich met eindige snelheid voortplant. Dat houdt in dat electromagnetische interactie niet een instantane-actie-op-afstand is. Tegelijk was de waarneming dat bij electromagnetische interactie impulsmoment behouden blijft. Om dat te verklaren moest worden verondersteld dat het electromagnetisch veld onafhankelijk impuls kan dragen. Dat wees erop dat het electromagnetisch veld niet zomaar een theoretische constructie is, maar dat het met materie gemeenschappelijk heeft dat het impuls kan dragen. Dat wijst erop dat een veld en materie niet zo verschillend zijn als men geneigd zal zijn te denken.

Inertie-veld

Aangezien in klassieke dynamica als aspecten van beweging worden begrepen in termen van eigenschappen van deeltjes die met velden interactie hebben, is het een natuurlijke gedachte om het bestaan van een inertie-veld te postuleren.

Om een indruk te krijgen van de eigeschappen van het inertie-veld, is het nuttig om het enigzins vergelijkbare fenomeen inductantie te bespreken. Een spoel van stroomgeleidende draad met zelf-inductie heeft de volgende eigenschap: de spoel zal weinig weerstand bieden aan electrische stroom, maar er zal verzet zijn tegen een verandering van stroomsterkte. (Als de stroomspoel wordt gekoeld tot aan een temperatuur waarbij supergeleiding optreedt zal de stroomspoel geen enkele weerstand tegen het lopen van een stroom hebben.) Het mechanisme van het verzet tegen een verandering is als volgt: een verandering van de stroomsterkte induceert een veranderend magnetisch veld, dat op zijn beurt een electisch veld induceert dat de verandering van stroomsterkte tegengaat.

In een draad met nul weerstand en nul zelf-inductie zal het aanleggen van een voltage resulteren in een onmiddelijke sprong naar een oneindig sterke stroom.
In een draad met enige weerstand en geen zelf-inductie zal het aanleggen van een voltage resulteren in een sprong naar een bepaalde stroomsterkte (waarbij de grootte van de stroomsterkte wordt beschreven door de wet van Ohm V = I * R )
In een draad zonder weerstand en enige zelf-inductie, en beginnend met een stroomsterkte van nul, zal het aanleggen van een voltage resulteren in een gestaag toenemende stroomsterkte. Dat wil zeggen: als zelf-inductie de enige factor is dan is de mate van verandering van stroomsterkte evenredig met het aangelegde voltage.

In het geval van het inertie-veld is er niet een mechanisme bekend. Het enige dat kan is de eigenschappen van de interactie van deeltjes met het inertie veld beschrijven. Dat is wat Newtons bewegingswetten doen.

Newton's bewegingswetten

Newtons bewegingswetten kunnen worden begrepen als de axioma's van een theorie van het inertie-veld

De eerste wet van Newton:
De keuze van euclidische geometrie om ruimte af te beelden is op zichzelf een fysische theorie. Het is alleszins begrijpelijk dat het gebruiken van euclidische geometrie niet werd beschouwd als een hanteren van een fysiche theorie, vanwege voor de hand liggende redenen dat er geen alternatief voor euclidische geometrie voorhanden was, en euclidische geometrie is perfect geschikt voor het doel. De eerste wet van Newton (in een her-interpretatie vanuit een modern gezichtspunt) stelt dat euclidische geometrie een passend model is voor de fysica van het inertie-veld. Als er geen kracht wordt uitgeoefend op een object (of wanneer de krachten die er op worden uitgeoefend in balans zijn) zal het object langs een euclidische rechte lijn bewegen.

De tweede wet van Newton:
Het inertie-veld gaat verandering van snelheid tegen. Om van snelheid ten opzichte van het inertie-veld te verandereren moet er een kracht worden uitgeoefend. De mate van verandering van snelheid evenredig met de aangelegde kracht.

De derde wet van Newton:
Het inertie-veld is symmetrisch voor alle richtingen en voor alle uniforme snelheden.
De oorspronkelijke formulering van de derde wet is dat er altijd behoud van impuls is: als object A een kracht uitoefent op object B, en beide objecten zweven vrij in de ruimte, dan zullen zowel object A als object B versnellen, en in dat proces zal de verandering van impuls van object A gelijk zijn aan de verandering van impuls van object B. Laat object A en object B een massa m_a respectievelijk m_b hebben en een versnelling a_a respectievelijk a_b ondergaan. Dan is het volgende geldig: m_a * a_a = m_b * a_b. Daaruit volgt dat de stelling F_ab = -F_ba (reactiekracht is altijd even sterk als de uitgeoefende kracht en in de tegenovergestelde richting) gelijkwaardig is aan stellen dat het inertieveld symmetrisch is voor alle richtingen en alle uniforme snelheden.

Een wezenlijk aspect van Newtons bewegingswetten is dat snelheid ten opzichte van het inertie-veld niet voorkomt in de axioma's van de theorie. Enkel de mate van verandering van snelheid maakt deel uit van de wiskundige structuur van de theorie.

Samenvattend:
De drie bewegingswetten van Newton kunnen worden begrepen als de axioma's van een theorie van het inertie-veld, en Newtons universele wet van zwaartekracht is een axioma van de theorie van het zwaartekrachtveld.

De equivalentie-klasse van inertiaalsystemen

De wetmatigheden van het inertie-veld en de wetmatigheid van zwaartekracht hebben gemeenschappelijk dat ze van toepassing zijn in de context van een specifieke klasse van coordinatensystemen: de klasse van inertiaalsystemen. Het criterium voor het onderscheid tussen een inertiaalsysteem en een niet-inertiaalsysteem is dat in een inertiaalsysteem de bewegingswetten van toepassing zijn.

(Vergelijk dit criterium met de situatie van electrische weerstand: R. De definitie van het begrip electrische weerstand is de wet van Ohm: R = V * I . Er bestaat niet zoiets als eerst de fysica van electrische weerstand definiëren, en vervolgens de wet van Ohm R = V / I ontdekken. In de fysica is het zo dat iedere geformuleerde wetmatigheid twee functies vervuld: als wetmatigheid en als operationele definitie van de specifieke context waarin die wetmatigheid van toepassing is.

Gezien vanuit relativistisch standpunt is het zo dat deze equivalentie-klasse van coordinatensystemen en het inertie-veld en Minkowski ruimtetijd effectief één en hetzelfde concept zijn. Ter vergelijking: van het electromagnetisch wordt aangenomen dat het aanwezig is in de ruimte, zoals deeltjes anwezig zijn in de ruimte. Het inertie-veld is niet aanwezig in de ruimte, vanuit relativistisch oogpunt bezien zijn het inertie-veld en ruimtetijd één en dezelfde entiteit.

Unificatie: algemene relativiteit

De algemene theorie van relativiteit is zowel een theorie van zwaartekracht als een theorie van beweging. In plaats van twee velden te postuleren, een inertie-veld en een zwaartekrachtveld, is het zo dat de algemene theorie van relativiteit het bestaan van een enkelvoudig veld verondersteld: het inertio-gravitationele veld. Het newtoniaanse conceptuele onderscheid tussen inertiële massa en gravitationele massa is niet van toepassing in algemene relativiteit. Met het postulaat van het inertio-gravitationele veld is het zo dat een onderscheid tussen inertiële massa en gravitationele massa niet voorkomt in de algemene theorie van relativiteit.

Om te zien hoe het mogelijk is om beginnend vanuit dat postulaat een theorie van zwaartekracht te formuleren is het nuttig om versnelling in Minkowski ruimtetijd te verkennen.

Versnellen in Minkowski ruimte-tijd

Afbeelding 1. Animatie
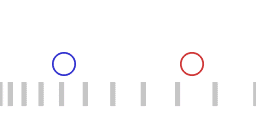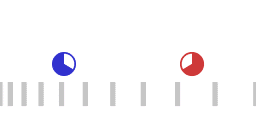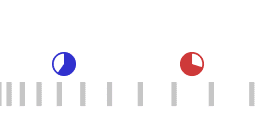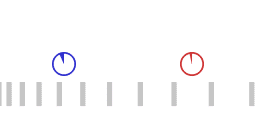
Twee versnellende ruimteschepen, het rode ruimteschip achtervolgt het blauwe ruimteschip.

Animatie 1 stelt twee versnellende ruimteschepen voor waarbij het "rode schip" het "blauwe schip" volgt. De twee ruimteschepen wisselen lichtsignalen uit (niet uitgebeeld in de animatie) om een constante onderlinge afstand te handhaven. Het rode schip past de eigen versnelling zodanig aan dat de reistijd van een heen-en-terug cyclus van het lichtsignaal hetzelfde blijft. Wanneer de heen-en-terug-tijd van het lichtsignaal hetzelfde blijft dan geldt het volgende:

Het rode schip is sterker aan het versnellen dan het blauwe schip, dat wil zeggen: op het rode schip is de G-kracht groter.
Signalen die zijn uitgezondendoor het "blauwe schip" zijn bij ontvangst door het "rode schip" blauwverschoven (zoals gemeten door de roden).
Signalen die zijn uitgezonden door het "rode schip" zijn bij ontvangst door het "blauwe schip" roodverschoven (zoals gemeten door de blauwen).
Voor de blauwen verstrijkt er meer eigentijd dan voor de roden.
Er verstrijkt een kleinere hoeveelheid eigentijd voor de roden, en daaruit volgt dat de roden een groter afstand afleggen dan de blauwen.

Animatie 1 geeft niet een Minkowski ruimtetijd diagram, weer, want in de animatie is er niet een globale coordinaat-tijd, en er is geen globale standaard van lengte. De verticale balken die van links naar rechts bewegen in de animatie representeren hoe de beweging van inertiaal bewegende objecten zou worden waargenomen door het rode en het blauwe schip.

Afbeelding 2. Animatie
Cirkelvormige bewering in Minkowski ruimte-tijd.

Animatie 2 toont twee ruimteschepen die langs een cirkelvormig traject bewegen. In deze aniamatie is de diameter van de cirkelvormige beweging nogal klein. Neem nu een cirkelvormige beweging met een extreem grote diameter in gedachten. De situatie is dat zeer dicht bij een toestand die niet te onderscheiden is van de situatie die wordt afgebeeld in animatie 1, die versnelling in rechte lijn afbeeldt. Dit niet te onderscheiden zijn kan worden gezien als een vorm van het principe van relativiteit van inertiaalbeweging. In het geval van beweging langs eencirklevomig pad is er een grote zijwaartse snelheid, een uniforme snelheid haaks op de richting van de versnelling. Maar in Minkowski ruimtetijd is uniforme snelheid relatief.

In de hierboven beschreven voorbeelden is de richting van oorzaak naar gevolg dat een object wordt versneld ten opzichte van het uniforme inertie-veld, en als gevolg darvan manifesteert inertie zich. De fundamentele aanname van de algemene theorie van relativiteit is dat massa het inertie-veld beinvloed. In aanwezigheid van gravitationele massa is het inertie-veld niet uniform, en deze vervorming van het inertie-veld treedt op als de overbrenger van zwaartekracht-interactie. Wanneer de hoeveelheid massa voldoende groot is, zoas de hoeveelheid massa van een planeet, zijn de effecten van de vervorming van het inertie-veld zeer merkbaar.

Afbeelding 3. Animatie
Een oneindig grote plaat materie genereert een uniform zwaartekracht.

Animatie 3 toont twee ruimteschepen en de grijze balk is een schematische weergave van een plaat materie die oneindig groot van afmeting is. Zo'n oneindige plaat materie zou de fysische eigenschappen van het inertio-gravitationele op een uniforme manier beinvloeden. Om hun afstand tot de plaat materie hetzelfde te houden moeten de ruimteschepen raketmotoren gebruiken. Net als in het geval van animatie 1 is het zo dat de animatie niet een Minkowski ruimtetijd diagram weergeeft, want er is niet een globale coordinaat-tijd en evenmin een globale standaard van lengte.

De aanname van slechts een enkel veld, het inertio-gravitationele veld, houdt in dat de situatie die is afgebeeld in animatie 3 equivalent moet zijn aan de situatie van animatie 1 in alle aspecten van fysica.

Het uniforme zwaartekrachtveld dat zich zou uitstrekken vanaf een oneindig grote plaat materie is fysisch niet realistisch, natuurlijk. Het doel van animaties 1, 2 en 3 is om de aandacht te richten op het concept van het inertio-gravitationele veld als één enkel veld, en om de eigenschappen daarvan te illustreren. Een uniform zwaartekrachtveld is op zichzelf niet detecteerbaar. Als de twee ruimteschepen uitsluitend tijdmetingen kunnen verrichten aan signalen die ze met elkaar uitwisselen (oftewel alleen lokale metingen) dan is de aanwezigheid of afwezigheid van de oneindig grote plaat materie inherent ondetecteerbaar. Gegeven de aanname van het enkelvoudige inertio-gravitationele veld is het bestaan van een uniform zwaartekrachtveld relatief.

Het zwaartekrachtveld dat zich uitstrekt vanaf een klomp materie zoals een planeet is een niet-uniform zwaartekrachtveld. Het zwaartekrachtveld dat zich uitstrekt vanaf een planeet wordt gekenmerkt door getijde-effecten, en die zijn niet relatief.

Gravitationele tijddilatatie

Afbeelding 4. Beeld
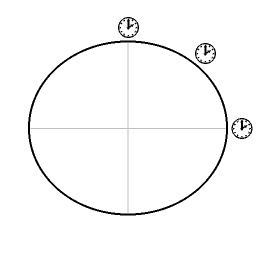
Klokken die zich op zee-niveau bevinden zullen overal ter wereld dezelfde hoeveelheid eigentijd tellen.

Afbeelding 4 toont de aarde, met de uitbuiking aan de evenaar zeer sterk overdreven. Voor klokken die zich op aarde bevinden zijn er twee factoren die die hoeveelheid eigentijd die verstrijkt bepalen. Eén factor daarvan is de gravitationele tijddilatatie. Klokken die zich op de polen bevinden zijn dichter bij het massamiddelpunt van de aarde; ze bevinden zich dieper in de potentiaalput, en dat correspondeert met een kleinere hoeveelheid eigentijd die verstrijkt, vergeleken met objecten die zich minder dicht bij het het centrum van aantrekking van de Aarde bevinden. De andere factor is snelheidgerelateerde tijddilatatie. Objecten die zich niet op de polen bevinden lopen in een grote cirkelbeweging rondom de aardas, en dat correspondeert met meer snelheidgerelateerde tijddilatatie (kleinere hoeveelheid eigentijd die verstrijkt) dan voor objecten die zich op de polen bevinden. Hoe dichter bij de evenaar, hoe meer snelheidgerelateerde tijddilatatie.

Voor alle klokken op aarde geldt dat de twee effecten, gravitationele tijddilatatie en snelheidsgerelateerde tijddilatatie precies tegen elkaar wegvallen, en voor alle klokken op aarde die zich op zee-niveau bevinden verstrijkt er dezelfde hoeveelheid eigentijd. Deze staat van dezelfde hoeveelheid eigentijd die overal op het gehele aardoppervlak verstrijkt is een staat waar het systeem zich van nature naartoe ontwikkeld. In de loop van honderden miljoenen jaren is de aarde langzamer gaan draaien. De aarde was vroeger dus sterker afgeplat dan tegenwoordig. Als de aarde langzamer gaat draaien, dan is de aarde naar verhouding te sterk afgeplat, en is er een spanning. In plaats van evenwicht is het dan zo dat aan de evenaar er meer eigentijd verstrijkt dan aan de polen. Die toestand van niet-evenwicht zal zich automatisch ontwikkelen naar een meer evenwichtige toestand: de mate van afplatting van de aarde neemt af, en de toestand ontwikkeld zich naar een staat waar op het gehele aardoppervlak overal dezelfde hoeveelheid eigentijd verstrijkt.

In de bovenstaande bespreking is alleen gravitationele tijddilatatie genoemd. Gravitationele tijddilatatie is één van de aspecten van kromming van ruimtetijd. Een theorie van zwaartekracht waar alleen maar gravitationele tijddilatatie in verwerkt zou zijn zou met name verkeerde voorspellingen opleveren bij zeer snelle beweging.
Algemene relativiteit beschrijft dat gravitationele afbuiging van licht dat rakelings langs de zon scheert 1.75 boogseconde zal zijn. Een zwaartekrachttheorie waar alleen maar gravitationele tijd dilatatie in verwerkt zit zou de helft van die waarde voorspellen: 0.83 boogseconde. Een voorbeeld van zo'n theorie met alleen gravitationele tijddilatatie erin verwerkt is een vroege verkennende theorie van Einstein, uit 1912.
Een theorie van zwaartekracht waar alleen maar gravitationele tijddilatatie in verwerkt zou zitten zou planeetbanen voorspellen die zeer dicht komen bij de banen die worden beschreven door newtoniaanse dynamica en algemene relativiteit, maar ze zou de precessie van de planeet Mercurius niet correct beschrijven.

Beweging langs een geodeet

Volgens de speciale theorie van relativiteit is er een verband tussen inertiaalbeweging en de hoeveelheid eigentijd. Waneer een verzameling mogelijke trajecten waarlangs een voorwerp/waarnemer van gebeurtenis A naar gebeurtenis B kan gaan wordt vergeleken, dan ziet men dat bij de beweging waarbij het voorwerp/de waarnemer de hele tijd in inertiaalbeweging waren het traject is waarop de grootste hoeveelheid eigentijd is verstreken.

Afbeelding 5. Beeld
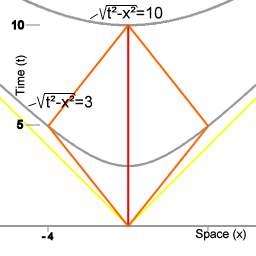
Het pad in ruimtetijd met alleen inertiaalbeweging (doorlopende rechte lijn in het diagram) correspondeert met een maximum in het verstrijken van eigentijd. Voor alle traject waarbij meer ruimtelijke afstand dan dat wordt afgelegd is het zo dat er minder eigentijd verstrijkt.

Volgens de algemene theorie kan inertiaalbeweging alleen beschreven worden in termen van dat verband tussen inertaalbeweging en de hoeveelheid eigentijd die verstrijkt. De algemene theorie beschrijft dat in aanwezigheid van inerte massa de fysische eigenschappen van ruimte-tijd vervormd zijn ten opzichte van de toestand van uniformiteit. Deze verandering van eigenschappen van ruimtetijd van, waarnaar wordt verwezen met de uitdrukking: 'kromming van ruimtetijd' treedt op als de overbrenger van zwaartekracht-interactie. Gegeven een zekere kromming van ruimtetijd, is een pad door de ruimtetijd dat van een afstand gezien niet-uniform is het pad met de de grootste hoeveelheid eigentijd.

De algemene theorie vervangt de eerste wet van Newton door een wetmatigheid die breder van toepassing is: voorwerpen in inertiaalbeweging bewegen langt een pad dat het pad is waarlangs de hoeveelheid eigentijd het grootste is.

John Wheeler heeft het voorbeeld geïntroduceerd van een tunnel die door het middelpunt van een planeet is geboord om het concept van bewegen langs een geodeet te illustreren.

Er wordt een tunnel geboord die twee punten op het oppervlak van een planeet verbindt die recht tegenover elkaar liggen. De diameter van de tunnel is zo klein in verhouding tot de afmeting van de planeet dat het verschil in massaverdeling verwaarloosbaar is.

Wanneer een capsule wordt losgelaten bij een toegang tot de tunnel zal die capsule vanaf dat moment in de tunnel heen en weer gaan. In het geval van de aarde zou de periode van oscillate ongeveer 90 minuten zijn, dezelfde tijdsduur voor een cyclus als voor een cirkelvormige baan om de aarde op zeer geringe hoogte. Gegeven de eigenschappen van de ruimtetijd waar de capsule zich in bevindt is het oscillerende pad het pad dat correspondeert met het pad met de grootste hoeveelheid eigentijd die verstrijkt. Zonder wrijving blijft de capsule van de ene ingang naar de andere ingang oscilleren, met enige wrijving zal de capsule uiteindelijk halverwege de tunnel (massamiddelpunt van de aarde) tot stilstand komen.)

Afbeelding 6. Animatie
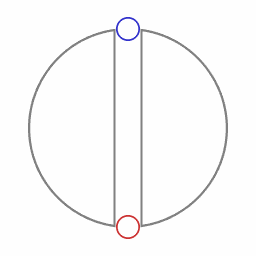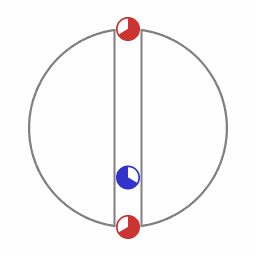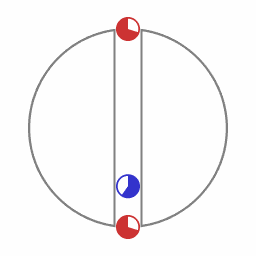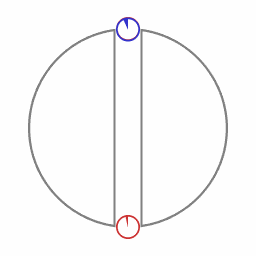
Het blauwe object volgt de wereldlijn waarop de hoeveelheid eigentijd verstrijkt het grootst is.

Analoog aan het woordgebruik in euclidische geometrie wordt dit pad dat correspondeert met een extremum een 'geodeet' genoemd. In euclidische geometrie is een geodeet een pad met de korts mogelijke ruimtelijke afstand. In de algemene theorie van relativiteit verwijst de uitdrukking 'geodeet' naar het pad met de grootst mogelijke hoeveelheid eigentijd.

Een versnellingsmeter aan boord van de capsule zou de hele tijd nul versnelling meten; de capsule die in de tunnel oscilleert is in inertiaalbeweging. Daartegenover staat dat voorwerpen die rusten op het oppervlak van de aarde niet in inertiaalbeweging zijn. Voor een voorwerp dat op het aardoppervlak rust geldt de inertiaalbeweging op die plaats een versnelling naar het centrum van de aarde is. Een voorwerp dat rust op het aardoppervlak wordt door door de normaalkracht die het aardoppervlak uitoefent versneld ten opzichte van een coordinatensysteem dat meebeweegt met de inertiaalbeweging op die plek.

In Minkowski ruimtetijd is de equivalentie-klasse van inertiaalsystemen universeel geldig. In ruimtetijd zoals door algemene relativiteit beschreven kan de equivalentie-klasse van inertiaalsystemen op het ene punt in de ruimte versnellen ten opzichte van de equivalentie-klasse van inertiaalsystemen op een ander punt in de ruimte. In het geval van het zonnestelsel kan er een hiërarchie worden onderscheiden. Een ruimtevaartuig in een baan om de Maan is in inertiaalbeweging. Het massamiddelpunt van de Maan is in inertiaalbeweging rondom het gemeenschappelijk massamiddelpunt van het aarde-maan-systeem. Het gemeenschappelijk massamiddelpunt van het Aarde-Maan-systeem is in inertiaalbeweging rondom de Zon. Het gemeenschappelijk massamiddelpunt van de alle objecten van het Zonnestelsel is in inertiaalbeweging rondom het middelpunt van het melkwegstelsel.

Analogieën tussen twee fundamentele unificaties

Afbeelding 7. Beeld
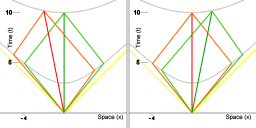
Ieder vlak van gelijktijdigheid kan worden gezien als een verschillende manier om een dwarsdoorsnede van Minkowski ruimtetijd te maken.

Afbeelding 7 is een illustratie die is gebruikt in het artikel over speciale relativiteit. Iedere relatieve snelheid heeft een corresponderende verdeling van coordinaat-tijd en coordinaat-afstand. Voor ieder(e) object/waarnemer in de ruimtetijd is er een specifiek vlak van gelijktijdigheid dat met het object/de waarnemer gelijk op loopt. Wat iedere waarnemer meet is een projectie van ruimtetijd in zijn eigen vlak van gelijktijdigheid. Iedere waarnemer heeft alleen direct zicht op een specifieke dwarsdoorsnede van de ruimtetijd: de dwarsdoorsnede die correspondeert mijn zijn vlak van gelijktijdigheid.

In het geval van het electromagnetisch veld is de snelheid van de waarnemer ten opzichte van het electromagnetisch veld de bepalende factor voor wat de waarnemer zal meten. In de vier-dimenstionale wereld van Minkowski ruimtetijd is het electromagnetisch veld een enkelvoudig veld. Voor iedere waarnemer zijn er ogenschijnlijk twee velden: een electrisch veld en een magnetisch veld. Voor waarnemers die met verschillende snelheid bewegen is het als het ware zo dat het electromagnetisch veld op verschillende manieren uiteenvalt in een electrische component en een magnetische component.

In het geval van het inertio-gravitationele veld is de bepalende factor voor wat een waarnemer zal meten de versnelling van de waarnemer ten opzichte van het veld. Voor waarnemers die versnellen ten opzichte van het inertio-gravitatinele veld met verschillende versnelling manifesteert het veld zich verschillend.

In het geval van klassieke electrodynamica is het technisch mogelijk om een theorie te formuleren waarin wordt aangenomen dat er daadwerkelijk een achtergrond aanwezig is van newtoniaanse absolute ruimte en absolute tijd. Een dergelijk type theorie is wordt vaak een 'ether theorie' genoemd; de term 'ether' verwijst dan naar het referentiekader dat verondersteld wordt aanwezig te zijn. Een dergelijke theorie staat voor de taak om een manier te vinden om de equivalentie van de klasse van inertiaalsystemen te verklaren. In een dergelijke ether theorie, is het zo dat een bepaalde snelheid ten opzichte van de ether resulteert in tijddilatatie en lengte-verkorting effecten die op zo'n manier optreden dat de veronderstelde newtoniaanse achtergrond geheel aan de waarneming wordt onttrokken. Iedere theorie die afzonderlijke ruimte en tijd aanneemt heeft aanvullende hypotheses nodig om te verklaren dat geen experiment ooit snelheid ten opzichte van de veronderstelde vaste newtoniaanse achtergrond heeft gemeten. De speciale theorie van relativiteit heeft geen aanvullende hypotheses nodig omdat snelheid ten opzichte van de ruimtetijd so wie so niet voorkomt in speciale relativiteit.

In het geval de theorie van speciale relativiteit is het technisch mogelijk om een theorie van beweging en zwaartekracht te formuleren waarin er wordt verondersteld dat er daadwerkelijk een achtergrond aanwezig is van onbeweeglijke Minkowski ruimtetijd. Dat wil zeggen: een theorie waarin een afzonderlijk inertie-veld en zwaartekrachtveld wordt verondersteld. Een dergelijke theorie staat voor de taak om een manier te vinden om de equivalentie van inertiële massa en gravitationele massa te verklaren. Het blijkt een theorie die uitgaan van een onbeweegelijke Minkowski ruimtetijd aangevuld moet worden met aannames van tijddilatetie en lengte-verkorting effecten die op zo'n manier optreden dat de veronderstelde Minkowski achtergrond geheel aan de waarneming wordt onttrokken. Iedere theorie die een afzonderlijk inertie-veld en zwaartekrachtveld verondersteld heeft aanvullend hypotheses nodig om te verklaren dat geen enkel experiment ooit versnelling ten opzichte van de veronderstelde onbeweegelijke achtergrond heeft gedetecteerd. De algemene theorie van relativiteit heeft zulke aanvullende hypotheses nodig omdat de veronderstelling van een onbeweeglijke achtergrond niet voorkomt in de algemene theorie.

Geen onbeweeglijke achtergrond-structuur

John Wheeler heeft de volgende zegswijze geïntroduceerd: "ruimtetijd vertelt inerte massa hoe het moet bewegen, en inerte massa verteld ruimtetijd hoe het moet krommen". Dat wil zeggen dat in de algemene theorie van relativiteit de kromming van de ruimtetijd een dynamische variabele is.

In newtoniaanse dynamics is het doel van het opschrijven en oplossen van de bewegingsvergelijking het vinden van de beweging van materiele objecten ten opzichte van de achtergrond. Het oplossen van bewegingsvergelijkingen in newtoniaanse dynamica kan in sommige situaties erg lastig zijn, maar er is tenminste een vaste achtergrond: inertie. In de algemene theorie van relativiteit is het doel van het opschrijven en oplossen van de veld-vergelijkingen het vinden van uitdrukkingen voor hoe de vorm van het inertio-gravitationele veld zich in de tijd zal ontwikkelen, en hoe de beweging van voorwerpen in de loop van de tijd zal ontwikkelen. Daarnaastishet zo dat potentiële zwaartekracht-energie bijdraagt aan de totale energie die in de berekening meegenomen moet worden. Dat wil zeggen: zoals alle vormen van energie die besloten zijn in een zeker volume aan ruimte heeft potentiële zwaartekracht-energie een zekere inertiële massa, en dus een zekere gravitationele massa, dus potentiële zwaartekracht-energie levert een bijdrage aan ruimtetijd kromming. Gezien deze complicerende factoren is het verbluffend dat het überhaupt mogelijk was om een theorie te formuleren.

De vergelijkingen van algemene relativiteit leunen op een verzameling verfijnde wiskundige gereedschappen die verregaande mogelijkheiden creëren voor het afhandelen van coördinatentransformaties. Daardoor kunnen de vergelijkingen uitgedrukt worden op een manier die zich op geen enkele manier vastlegt wat betreft de keuze van coordinatensysteem. De klasse van manieren om ruimte af te beelen met een coordinatensysteem wordt de diffeomorfisme-klasse genoemd. De systemen van deze klasse kunne in elkaar worden getransformeerd door een transformatie die het "weefsel" van de ruimtetijd niet "scheurt" of "knipt". Dat wil zeggen: twee punten in de ruimtetijd die naburige punten zijn in een lid van de diffeomorfisme klasse zijn ook naburige punten in alle andere leden vande diffeomorfisme klasse. Die restrictie in acht nemend is het zo dat het wiskundige apparaat een enorme diversiteit aan tranformaties ondersteund: translatie, uniforme versnelling, willekeurig versnelling, draaing met constante hoeksnelheid, draaing met variabele hoeksnelheid, iedere deformatie die een "verbuiging" inhoud, enz.

Het gebruiken van het wiskundige apparaat dat het mogelijk maakt om vergelijkingen zo te formuleren dat ze niet zijn vastgelegd op een bepaalde keuze van coordinatensysteem (uit de diffeomorfisme klasse) wordt 'coordinaat-onafhankelijke vergelijkingen' genoemd. De algemene theorie van relativiteit gebruikt coordinaat-onafhankelijke vergelijkingen om bepaalde fysische eigenschappen uit te drukken. De fysica van 'inerte masse vertelt ruimtetijd hoe ze moet krommen, en gekromde ruimtetijd vertelt inerte massa hoe te bewegen' kan worden uitgedrukt op een coordinaat-onafhankelijke manier. De wiskundige kracht van een coordinaat-onafhankelijk representatie maakt het mogelijk om ondanks het feit dat de achtergrond zelf een dynamische variabele is toch vergelijkingen te formuleren.

Wanneer er een oplossing voor de vergelijkingen is gevonden is de laatste stap het kiezen van een coordinatensysteem en het afbeelden van de oplossing op dat coordinatensysteem.

Materie, energie, velden en ruimtetijd

In de introductie is vermeld dat het electromagnetisch impuls kan overdragen, wat erop wijst dat velden en materie niet zo verschillend zijn als men geneigd zou zijn te denken.

Electrodynamica beschrijft dat een oscillerend geladen deeltje electromagnetische golven zal uitstralen. Het proces van electromagnetische golven uitstralen verminderd de kinetische energie van het oscillerende deeltje.

De algemene theorie van relativiteit beschrijft dat wanneer twee massa's rondom elkaar bewegen in een niet-cirkelvormige baan het systeem als geheel zwaartekrachtgolven zal uitzenden. Met andere woorden: zwaartekracht golven (zich voortplantende schommelingen van het inertio-gravitationele veld) voeren energie en impuls weg van een systeem van om elkaar bewegende massa's. De algemene theorie van relativiteit geeft aan dat materie, energie, velden en ruimtetijd niet zo verschillend van elkaar zijn als men geneigd zal zijn te denken.

Bronnen van dit artikel

Een belangrijk bron van informatie, aanvullend op de standaard leerboeken (Misner, Thorne and Wheeler etc.), waren artikelen van wetenschapshistorici zoals Michel Janssen , John Stachel , John Norton , Jürgen Renn , en anderen. Wetenschapshistorici zijn er meer dan leerboek-schrijvers op gespitst om de onderliggende concepten te bespreken die een motivatie waren voor fysici om de wegen te verkennen die ze hebben verkend.

John Norton:
'What was Einstein's principle of Equivalence?' (PDF-document, 376 KB) John Norton bespreekt dat de versie van het principe van equivalentie die meestan wordt geboden in exposities van algemene relativiteit fundamenteel verschillend qua inhoud ten opzichte vanhet principe dat Einstein in zijn artikelen presenteerde. Norton is van oordeel dat Einsteins versie te prefereren is. Download van pitt.edu

'General Covariance and the Foundations of General Relativity: Eight Decades of Dispute' (PDF-document, 460 KB) Download van pitt.edu

De uitdrukking 'inertio-gravitationeel veld

Bij mijn weten is de uitdruking inertio-gravitationeel veld geïntroduceerd door John Stachel. Met name de auteurs John Stachel en Michel Janssen gebruiken het om onderliggende concepten te verhelderen. De uitdrukking 'inertio-gravitationeel veld' past als een handschoen, en ik verwacht dat in de komende jaren het een standaard uitdrukking zal worden in het onderwijs van relativistische fysica.

Essay van John Stachel waarin hij pleit voor de interpretatie van de Algmene Theorie van Relativiteit in termen van een inertio-gravitationele structuur:
The Story of Newstein Or: Is Gravity Just another Pretty Force?
Gepubliceerd in: The Genesis of General Relativity, Vol 4.
Redacteurs: Jürgen Renn, John Stachel, Michel Janssen, John Norton, Tilman Sauer.

Lijst van publicaties die via internet gedownload kunnen worden waarin de uitdrukking 'inertio-gravitationeel veld' wordt gebruikt:

John Stachel

• Structure, Individuality and Quantum Gravity (PDF-document, 333 KB) Download van arxiv.org
  
• The Hole Argument for Covariant Theories (PDF-document, 176 KB) Download van arxiv.org

Michel Janssen

• Einstein's first systematic exposition of general relativity (PDF-document, 187 KB) Michel Janssen bespreekt de concepten in Einsteins presentatie. Download van philsci-archive.pitt.edu
  
• Relativity (PDF-document, 88 KB) Artikel over relativiteit voor de Dictionary of the History of Ideas Download van philsci-archive.pitt.edu
  
• The Einstein-Besso Manuscript: A Glimpse Behind the Curtain of the Wizard (PDF-document, 1.3 MB) Download van tc.umn.edu
  
• A Journey More Important Than Its Destination: Einstein’s Quest for General Relativity,1907–1920. (PDF-document, 1.7 MB) Een serie dia's met afbeeldingen en korte stukje tekst om de ontwikkeling van ideeën te illustreren. Download van tc.umn.edu

Oliver Pooley

• 'Lecture 4: General Covariance and gauge theories'(PDF-document, 107 KB) Download van users.ox.ac.uk

Tekst, afbeeldingen en animaties zijn beschikbaar gesteld voor anderen onder de volgende voorwaarden:
Creative Commons Attribution-ShareAlike 3.0 Unported License.

Laatste keer dat deze pagina is bewerkt: 18 juni 2017.