Speciale Relativiteit
De ontwikkelingsstadia in de geschiedenis van fysica kunnen worden onderscheiden in fases van toenemend inzicht in de centrale positie van inertie. Achteraf gezien kan worden herkend dat de copernicaanse revolutie de eerste stap was in het herkennen van inertie als het organiserende principe van the fysica van beweging.
Galileï wees erop waarom het mogelijk is om wetmatigheden van beweging te formuleren. Denk je in dat je je bevindt in de hut van een boot die aan het varen is over volledig vlak water. Je bent aan het jongleren, of je bent darts aan het gooien, of een dergelijke handeling. (Galileï gebruikte andere voorbeelden, maar dat maakt niet uit voor de inhoud van de argumentatie.) Galileï voerde aan: wat de snelheid van de boot ook is, de timing voor het jongleren of het werpen van de darts is hetzelfde. Dit illustreert dat er wetmatigheden van beweging zijn, en een vaardig jongleur worden bestaat uit het verwerven van impliciete kennis (motorische kennis) van hoe om te gaan met de wetmatigheden van beweging.
Het raster van het dartbord dient als een referentie, de darter mikt de pijlen ten opzichte van dat referentiesysteem. Eén laag van 'hetzelfde' is dat het er niet toe doet waar in de ruimte het dartbord staat opgesteld, de wetmatigheden van beweging zijn hetzelfde. Een tweede laag is dat de snelheid van een boot ten opzichte van een andere boot er evenmin toe doet, de wetmatigheden van beweging zijn hetzelfde.
Symmetrie van inertie
Als je een kracht uitoefend op een voorwerp, met versnelling ervan als gevolg, dan geeft in alle richtingen dezelfde kracht dezelfde versnelling; inertie is isotroop. (Isotropie = hetzelfde in alle richtingen). Inertie is symmetrisch voor alle plaatsen en oriëntaties in de ruimte. Bovendien is inertie symmetrisch voor alle uniforme snelheden. Probeer je eens een voorstelling te maken van het tegenovergestelde, stel je eens voor dat inertie wispelturig zou zijn, veranderend van plek naar plek en van het ene moment op het andere - beweging zou dan zonder wetmatigheden zijn. Maar inertie is buitengewoon symmetrisch. Vanwege die verregaande symmetrieën is het formuleren van bewegingswetten een vruchtbare onderneming.
Een theorie van beweging beschrijft de eigenschappen van inertie; om een theorie van beweging te formuleren moeten de symmetrieën van inertie belichaamd worden. In de tijd dat een wiskundige bewegingstheorie werd geformuleerd, uitmondend in het werk van Isaac Newton, was dat belichamen rechttoe-rechtaan: euclidische ruimte heeft dezelfde symmetrieën als inertieruimte.
Achteraf kunnen we herkennen dat de copernicaanse revolutie een verandering bracht in de rol die geometrie speelt in de fysica. In de oudheid was geometrie een instrument om vormen te beschrijven, de baan van een planeet werd gedacht als een vorm, en die vorm werd beschreven met geometrie. Maar in newtoniaanse dynamica speelt de euclidische geometrie een veel diepgaander rol. In newtoniaanse dynamica is inertie het primaire organiserende principe, en terugkijkend kunnen we herkennen dat euclidische geometrie passend is omdat het een perfect model is voor de symmetrieën van inertie. Het gebruiken van euclidische geometrie als instrument om beweging te beschrijven is feitelijk het aannemen van een fysische theorie.
Stilzwijgende aannames
Euclidische geometrie gebruiken als integraal onderdeel van een theorie van beweging houdt in dat drie aspecten als hetzelfde worden beschouwd:
- Fysische ruimte, de arena waarin fysische verschijnselen zich afspelen.
- Inertiaalruimte, de bron van inertie.
- Euclidische ruimte, een specifiek (wiskundig) concept van ruimte.
Het gelijkstellen van deze drie was eeuwenlang een stilzwijgende aanname van klassieke mechanica. Of beter, de mogelijkheid dat in bovenstaande drie concepten zou kunnen worden gedifferentiëerd werd niet besproken. De introductie van speciale relativiteit bracht daar verandering in.
Opmerking: natuurkundigen maken zeer zelden onderscheid tussen fysische ruimte en inertiaalruimte, en het is ook niet nodig om dat te doen. In de drie gevestigde theorieën van beweging, newtoniaanse mechanica, speciale relativiteit en algemene relativiteit, worden fysische ruimte en inertiaalruimte gelijkgesteld.
Equivalentieklasse van coördinaatsystemen
De euclidische ruimte wordt weergegeven met een coördinatensysteem (een coördinatenraster). Een coördinatensysteem heeft een nulpunt het heeft richting. De alomvattende weergave van de symmetrieën van inertie moeten worden opgegeven als een equivalentieklasse van coördinatensystemen.
Lineaire transformaties
De transformaties die leden van de equivalentieklasse van inertiale coördinatensystemen relateren moeten lineaire transformaties zijn. (Het hoeft geen betoog dat transformaties die kwadratische of hogere uitdrukkingen bevatten, waardoor ze niet-lineair zijn, niet voldoen aan de geeiste symmetrieën.) Om precies te zijn, de symmetrie-vereisten reduceren de transformaties tot de volgende:
- Transformaties tussen coördinatensystemen die een hoek maken ten opzichte van elkaar.
- Transformaties tussen coördinatensystemen die ten opzichte van elkaar verschoven zijn.
- Transformaties tussen coördinatensystemen die een uniforme snelheid hebben ten opzichte van elkaar.
Voor ieder voorwerp dat in inertiaalbeweging is is er een coördinatensysteem dat met dat voorwerp meebeweegt. Dat houdt in dat de wetmatigheid die het optellen van snelheden beschrijft en de wetmatigheid die de transformatie beschrijft één en dezelfde wetmatigheid zijn.
Speciale relativiteit
De speciale theorie van relativiteit is, net als Newton's bewegingswetten, een theorie van beweging: het gaat over relaties tussen ruimte, tijd, en materie.
Net als in het geval van Newton's bewegingswetten gebruikt speciale relativiteit het fenomeen inertie als het primaire organiserende principe voor het begrijpen van bewegingsleer, maar dan op een dieper niveau. Het doel van dit artikel is om dat te demonstreren.
Synchronisatie procedure

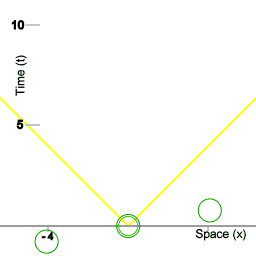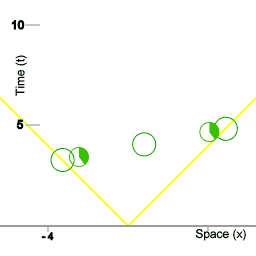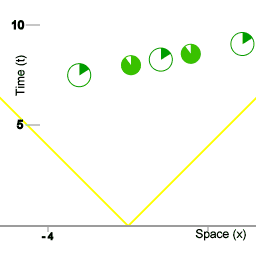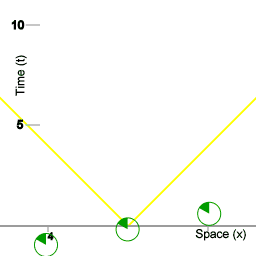
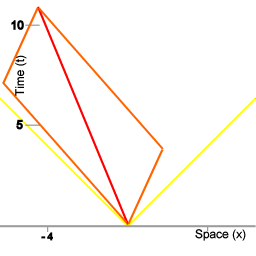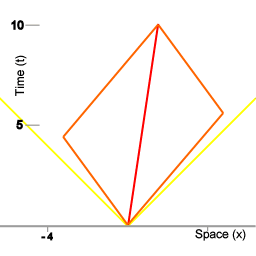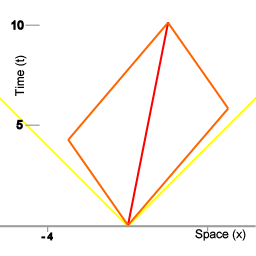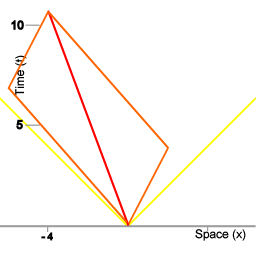
Drie klokken.
Beeld 1 is een weergave van drie klokken, die tijd tellen. Om ervoor te zorgen dat die klokken perfect gelijk blijven lopen heb je een manier nodig om tijd te verspreiden. Een manier daarvoor is door met lichtpulsen te werken, ik kom daar later op terug. De volgende animatie toont de drie klokken, met kleinere klokken die op en neer reizen.
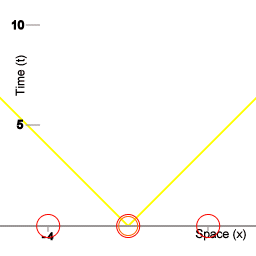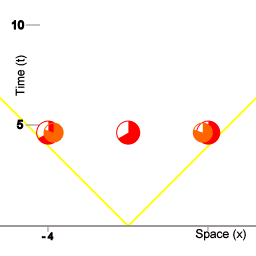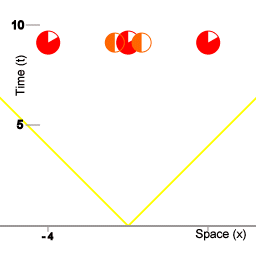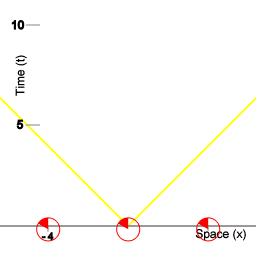
Drie ruimteschepen en een procedure om gesynchroniseerde vloottijd te handhaven.
De eerste animatie geeft een ruimtetijd diagram weer. De gele lijnen stellen de wereldlijnen voor van pulsen van licht die op het tijdstip t=0 worden uitgezonden. De opeenvolgende beeldjes van de animatie tezamen vormen de weergave van een enkel diagram.
Een waarnemer kan altijd zijn eigen positie definiëren als de oorsprong van een coördinatensysteem waarin posities van ander objecten kunnen worden afgebeeld, zoals de schepen van een vloot van ruimteschepen. In de animaties van dit artikel bestaat de vloot uit drie schepen, maar het kan ieder aantal schepen zijn, en die verzameling schepen kan dan worden gedacht als punten van een raster. Dat raster voorziet dan in een coördinatensysteem om aan gebeurtenissen een coördinaat afstand en een coördinaat tijdsduur toe te kennen.
Ieder schip van de vloot houdt een logboek bij van gebeurtenissen die plaatsvinden op de ruimte coördinaat van dat schip, waarbij van iedere gebeurtenis het punt in vloottijd wordt vastgelegd. De schepen van de vloot spelen deze logboeken aan elkaar door, en op ieder schip van de vloot kan de informatie in de ontvangen logboeken samengevoegd worden tot een alomvattende ruimtetijd-afbeelding van de gebeurtenissen. Animatie 2 is een voorbeeld van zo'n alomvattende afbeelding
De drie rode cirkels stellen een vloot van ruimteschepen voor. De cirkels met veranderende segmenten erin stellen klokken voor die zich aan boord van de schepen bevinden. De twee oranje cirkels stellen miniklokken voor die heen en weer vliegen tussen de schepen van de vloot; de miniklokken worden gebruikt voor een procedure om gesynchroniseerde vloottijd te handhaven. De synchronisatie procedure die hier wordt gebruikt maakt gebruikt van de isotropie van inertie. De schepen van de vloot zorgen ervoor dat de miniklokken in beide richtingen met dezelfde kracht worden weggestuurd. (Om preciezer te zijn: alle miniklokken hebben dezelfde massa, en bij het wegschieten van de miniklokken wordt aan iedere miniklok precies evenveel kinetische energie overgedragen.)
De onderlinge afstand tussen de schepen van de vloot is 4 eenheden van afstand. In deze situatie houdt '4 eenheden van afstand' in dat lichtpulsen er vier eenheden van tijd over doen om zich van het ene schip naar het andere voort te planten. In dit artikel wordt afstand steeds gemeten in termen van tijd: de hoeveelheid tijd die lichtpulsen onderweg zijn. In deze animatie doen de miniklokken er 5 eenheden van vloottijd over om van het ene schip naar het andere te reizen, dus hun snelheid ten opzichte van de vloot is 4/5e de snelheid van het licht. De duur van de reis van het ene schip naar het volgende is voor de miniklokken zelf 3 eenheden van eigen-tijd. Dus in deze animatie is de tijd dilatatie het verschil tussen 5 eenheden van vloottijd voor één helft van de procedure, en 3 eenheden van tijd voor de miniklokken.
Transmissie-achterstand is niet fundamenteel
Lichtpulsen hebben een zekere voortplantingssnelheid; hoe groter de afstand die het licht moet afleggen, hoe langer de benodigde tijd, dus informatie die van ver komt, komt met een corresponderende tijd-achterstand binnen. Het is belangrijk om op te merken dat deze transmissie-achterstanden geen rol spelen in speciale relativiteit. Er moet rekening mee worden gehouden, natuurlijk, in het samenstellen van een alomvattende ruimtetijd afbeelding, maar de inhoud van speciale relativiteit begint pas nadat transmissie-achterstanden zijn verrekend. Om toe te spitsen op het relativistische effect is de animatie erop gericht om waarnemings verschillen die teruggaan op transmissie-achterstand te vermijden.
Geen verklaring
De speciale theorie van relativiteit voorziet niet in een verklaring voor het waarom van die tijddilatatie. Het beginpunt van relativistische fysica is te veronderstellen dat het zo gaat, en de inhoud van de theorie bestaat eruit dat de consequenties van dat gegeven in alle richtingen worden uitgewerkt. De rechtvaardiging berust op het succes van relativistische theorie in toegepaste fysica.
Minkowski ruimtetijd geometrie
De conceptuele verschuiving in de overgang van klassieke mechanica naar de ruimtetijd van speciale relativiteit is een verschuiving van euclidische ruimte en tijd naar Minkowski ruimtetijd.
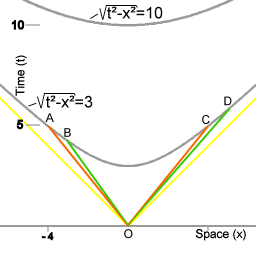
De chrono-geometrie van ruimtetijd intervallen.
De lijn waarop de punten A, B, C en D zich bevinden verbindt alle punten in de ruimtetijd die gemeenschappelijk hebben dat voor een voorwerp dat met constante snelheid vanaf punt O in ruimtetijd naar een punt op die lijn beweegt er 3 eenheiden van eigen-tijd verstrijken. Bijvoorbeeld, de lijnen OA en OC in afbeelding 3 corresponderen met de wereldlijnen van de miniklokken in animatie 2.
Ruimtetijd interval
Het concept van ruimtetijd-interval is enigzins analoog aan het concept van radiale afstand in euclidische ruimte. In euclidische ruimte met twee dimensies van ruimte is er de relatie:
En dat is natuurlijk de welbekende stelling van Pythagoras.
De radiale afstand tussen twee punten in de ruimte is een invariant, in de zin dat ze onafhankelijk is van de specifieke manier om ruimte in kaart te brengen met een euclidisch coördinatensysteem. Radiale afstand tussen twee punten is invariant onder een coördinatentransformatie die correspondeert met een ruimtelijke draaing.
In dit artikel wordt het woord 'ruimte' in een zeer abstracte zin gebruikt, in een betekenis die aanzienlijk verschilt van die alledaagse betekenis van dat woord. In dit artikel wordt alles in termen van tijd beschreven. Ruimtelijke afstand wordt gemeten in termen van de tijdsduur die licht nodig heeft om de afstand te overbruggen. Tijd en ruimtelijke afstand worden allebei in eenheden van tijd geteld.
Het invariante ruimtetijd interval van Minkowski ruimtetijd geometrie belichaamt een relatie tussen ruimte en tijd. De grootte van het ruimtetijd interval wordt geteld in eenheden van tijd: de eigentijd zoals gemeten door klokken die meebewegen. Het symbool voor eigentijd is τ (the Griekse letter 'tau'.)
Het radikale verschil is de aanwezigheid van het min-teken.
Bij een geometrische weergave is het ruimtetijd interval geassociëerd met een hyperbool curve, zoals getoond in afbeelding 2, terwijl radiale afstand in euclidische ruimte natuurlijk met een cirkel geassociëerd is. Merk op dat afbeelding 3 een Minkowski ruimte in kaart brengt in een euclidische ruimte; het is niet een directe afbeelding van Minkowski ruimte.
Metriek van Minkowski ruimtetijd
In de context van euclidische ruimte is er een natuurlijk concept van afstand tussen twee ruimtelijke punten: de radiale afstand. Dit concept van radiale afstand wordt 'de metriek van de Euclidische ruimte' genoemd, omdat het een maat is voor ruimtelijke afstand.
In het geval van Minkowski ruimtetijd is het gebruikelijk om naar de eigenschappen ervan te verwijzen als 'geometrie van Minkowski ruimtetijd. (Een meer accurate uitdrukking zou zijn 'chrono-geometrie van Minkowski ruimtetijd', maar die uitdrukking wordt maar zelden gehanteerd.) Per analogie met het concept van een metriek in euclidische context wordt er naar de formule voor het invariante ruimtetijd-interval verwezen als 'de metriek van Minkowski ruimtetijd'.
De uitdrukking 'metriek van Minkowski ruimtetijd' is een gebruikelijke vorm, maar vanwege het verschil met het algemene concept van een metriek wordt er ook wel naar verwezen als een pseudo-metriek. Hiermee wordt aangegeven dat in wiskundige uitdrukkingen de pseudo-metriek wel de zelfde functie vervuld als een metriek, het toch iets fundamenteel anders is als een metriek.
Het concept van een metriek kan in vele verschillende geometrische contexten worden toegepast. Een simpel voorbeeld van een metriek is de metriek van de manier waarop in het schaakspel de koning beweegt. Om langs een kolom of rij bewegend van de ene hoek in de andere te komen zijn 7 stappen nodig, en om diagonaal naar te hoek tegenover te gaan is ook 7 stappen. Die metriek is een voorbeeld van een non-euclidische metriek, want de stelling van Pythagoras gaat niet op.
Voor de metriek van Minkowski ruimtetijd, waarbij het kwadraat van de ene dimensie wordt afgetrokken van het kwadraat van een andere dimensie, is er niet een verklaring. Er is geen theorie waarmee de vraag wordt aangesproken hoe de structuur van ruimte en tijd zo in elkaar kan zitten. De huidige situatie is dat de eigenschappen van Minkowski ruimtetijd als een gegeven aangenomen moeten worden om überhaupt een theorie te kunnen formuleren.
Ruimtetijd interval
Speciale relativiteit impliceert dat het ruimtetijd interval fundamenteler is dan ruimtelijke afstand. Speciale relativiteit impliceert dat ruimte niet kan worden gedacht als een entiteit met een onafhankelijk bestaan. In plaats daarvan voelen fysici zich genoodzaakt om ruimte te zien als een soort 3D silhouet van een fundamenteler entiteit: het ruimtetijd continuüm, waarbij het gaat om drie ruimtelijke dimensies en één tijddimensie. Afhankelijk van hoe de ruimtetijd wordt afgebeeld komen afstanden verschillend uit, op een manier die doet denken aan geometrische projectie.
Equivalentie van verschillende coördinaat-afbeeldingen
Drie ruimteschepen en een procedure om gesynchroniseerde vloottijd te handhaven.
De drie donkergroene cirkels beelden een vloot van ruimteschepen uit. Net als in de eerste animaties zijn er miniklokken die heen en weer schieten als onderdeel van een procedure om gesynchroniseerde vloottijd te handhaven. De trajecten van de groene miniklokken corresponderen met de wereldlijnen OB en OD in afbeelding 3.
Dit ruimtetijd diagram geeft weer hoe de beweging van de groene vloot in ruimtetijd wordt afgebeeld in een coördinatensysteem dat een snelheid van 2/5e van de lichtsnelheid beweegt ten opzichte van de groene vloot.
De procedure werkt voor de groene vloot precies zo als voor de rode vloot in de eerdere animatie. Het centrale schip zend de miniklokken weg in tegenovergestelde richtingen en iedere miniklok heeft een relatieve snelheid van 4/5 van de lichtsnelheid ten opzichte van de vloot. Voor iedere etappe van de procedure verstrijkt er voor de miniklokken 3 eenheden eigen-tijd, en de schepen van de vloot tellen 5 eenheden eigen-tijd voor iedere etappe van de procedure.
Symmetrie
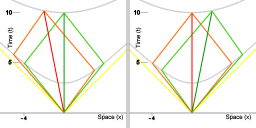
Deze afbeelding toont ruimtetijd diagrammen die zowel de procedure van de rode vloot en de procedure van de groene vloot in kaart brengen. Het diagram links toont een weergave van gebeurtenissen in ruimtetijd in een coördinatensysteem dat met de groene vloot meebeweegt, het diagram aan de rechterkant toont een afbeelding van gebeurtenissen in ruimtetijd in een coördinatensysteem dat met de rode vloot meebeweegt.
In dit geval is de synchronisatie procedure en de afbeelding ervan in een ruimtetijd diagram geïntroduceerd vanuit de rode vloot, waarbij de fysica werd afgebeeld in een coördinatensysteem dat meebeweegt met de rode vloot. Het had ook met de groene vloot eerst geïntroduceerd kunnen worden, waarbij de fysica wordt afgebeeld in een coördinatensysteem dat meebeweegt met de groene vloot. Volgens speciale relativiteit is er volledige symmetrie tussen de twee coördinaat-afbeeldingen.
Equivalentie klasse van coördinatensystemen
Equivalentie klasse van coördinaten-systemen.
In animatie 5 wordt de complete symmetry van afbeelding 5 geïllustreerd in de vorm van een animatie. De reeks van frames is hier een opeenvolging van coördinatensystemen met een snelheid ten opzichte van elkaar. Ieder frame geeft dezelfde reeks gebeurtenissen weer: de synchronisatieprocedure zoals die is beschreven. Alle afzonderlijke frames van de animatie geven een even goede weergave van de fysica. De verzameling van alle frames is een representatie van een equivalentieklasse van coördinatensystemen.
Met name het ruimtetijd-interval is hetzelfde in alle weergaven van de ruimtetijd. Echter, in ieder frame is gelijktijdigheid verschillend.
Relativiteit van gelijktijdigheid
Een stilzwijgende aanname in klassieke mechanica is dat beweging en gelijktijdigheid verschillende entiteiten zijn. Die aanname kan niet meegenomen worden naar speciale relativiteit. Er is geen inherent criterium om twee gebeurtenissen als al dan niet gelijktijdig te beschouwen; de relativiteit van gelijktijdigheid.
Hoewel er geen inherent criterium is om gelijktijdigheid toe te schrijven, er is wel een criterium dat kan worden omschreven als een "zuinigheidscriterium". Als je als definitie van gelijktijdigheid bovenstaande synchronisatie procedure neemt (synchronisatie die de symmetrieën van inertie als referentie neemt), dan krijgen de wetten van de fysica, zoals de vergelijkingen voor electromagnetisme, hun simpelste vorm.
Vergelijking: lichtdragende ether en Minkowski ruimtetijd
De diagramme 7 tot en met 10 zijn een reeks van afbeeldingen van een synchronisatie procedure. De gele lijnen beelden wereldlijnen van lichtpulsen uit.
In de voorgaande voorbeelden werden voor de synchronisatie procedure miniklokken gebruikt. Het voordeel daarvan is dat bij iedere aankomst je precies kan zien hoeveel eigentijd er voor de miniklokken is verstreken tijdens hun reis, waardoor je in staat bent de betrouwbaarheid van de synchronisatie te verifiëren. Bij iedere aankomst wordt gecontroleerd of er voor iedere miniklok even grote hoeveelheid eigentijd is verstreken tijdens de reis.
Bij het synchroniseren met lichtpulsen is die informatie niet beschikbaar: een eventueel verschil in reistijd kan niet geconstateerd worden.
Klassieke fysica
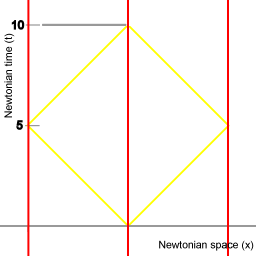
Beeld 7. Diagram
The synchronisatie procedure in klassieke ruimtetijd, met lichtpulsen. De procedure neemt 10 eenheden van tijd in beslag. |
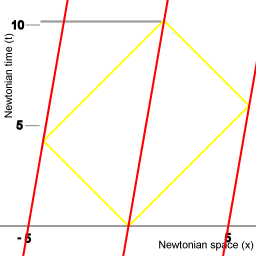
Afbeelding 8. Diagram
Het geval van een vloot met een snelheid ten opzichte van de ether: het duurt langer dan 10 eenheden van tijd om de procedure te doorlopen. |
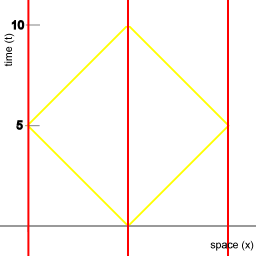
Beeld 9. Diagram
De synchronisatie procedure in Minkowski ruimtetijd. Het coördinatensysteem beweegt mee met de vloot. De procedure neemt 10 eenheden van tijd in beslag. |
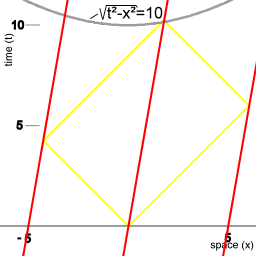
Afbeelding 10. Diagram
De synchronisatie procedure afgebeeld in een coördinatensysteem dat beweegt ten opzichte van de vloot. Het duurt precies tien eenheden van vloottijd om de procedure te doorlopen. |
Diagrammen 7 en 8 geven weer wat je verwacht dat er zal gebeuren als de lichtsignalen geacht worden zich voort te planten in een medium, dit medium kan de 'lichtdragende ether' worden genoemd. Als de vloot van ruimteschepen een snelheid heeft ten opzichte van de lichtdragende ethere dan zal de totale afgelegde afstand van de lichtsignalen groter zijn, en de procedure zal meer tijd in beslag nemen dan wanneer de ruimteschepen stilstaan ten opzichte van de lichtdragende ether.
Minkowski ruimtetijd
Diagrammen 9 en 10 geven weer wat je verwacht dat er zal gebeuren als het geheel zich afspeelt in Minkowski ruimtetijd. Iedere afbeelding van de procedure zal aangeven dat er 10 eenheden van eigentijd zullen verstrijken. Met andere woorden, de synchronisatie procedure zal geen informatie verschaffen over een snelheid ten opzichte van enige achtergrondstructuur.
Einstein synchronisatie procedure
Wanneer lichtpulsen worden gebruikt voor het synchroniseren van klokken wordt het 'Einstein synchronisatie procedure' genoemd. In het artikel, 'Zur Electrodynamik bewegter Körper', waarin Einstein speciale relativiteit introduceerde poneerde hij die synchronisatie procedure als definitie van gelijktijdigheid.
De diagrammen illustreren in welke omgeving de Einstein synchronisatie procedure van toepassing is. In ruimte en tijd zoals men het zich voorstelde vóór speciale relativiteit verwacht je dat de synchronisatie procedure meer tijd in beslag zal nemen als de zenders/ontvangers een snelheid hebben ten opzichte van de lichtdragende ether. Aan de hand van dat verschil zal je kunnen herleiden welke snelheid correspondeert met stilstaan ten opzichte van de lichtdragende ether, en dat is dan de referentie voor gelijktijdigheid. In Minkowski ruimtetijd daarentegen, is de Einstein synchronisatie procedure de passende aanpak.
Symmetrische snelheid-gerelateerde tijddilatatie

De situatie is symmetrisch. De rode vloot en de groene vloot hebben een snelheid ten opzichte van elkaar, dus voor iedere eenheid van rode-vloot-tijd verstrijkt er minder dan één eenheid van groene-vloot-tijd, en voor iedere eenheid van groene-vloot-tijd verstrijkt er minder dan één eenheid van rode-vloot-tijd.
Op het tijdstip t=0 passeren de twee centrale schepen van de beide vloten elkaar. Laat het rode schip op t=0 een signaal uitzenden met een bepaalde frequentie zoals gemeten ten opzichte van rode-vloot-tijd. Het groene schip ontvangt dat signaal, en dat signaal zal, gemeten ten opzichte van groene-vloot-tijd, naar een lagere frequentie verschoven zijn.
En omgekeerd: laat het groene schip op t=0 een signaal uitzenden met een bepaalde frequentie zoals gemeten ten opzichte van groene-vloot-tijd. Het rode schip ontvangt dat signaal, en dat signaal zal, gemeten ten opzichte van rode-vloot-tijd, naar een lagere frequentie verschoven zijn.
Dit type tijddilatatie wordt 'symmetrische snelheid-tijddilatatie' genoemd.
Een voorbeeld daarvan zijn de trajecten van de tijd-verspreidende miniklokken in de animaties. De miniklokken hebben de hele tijd een snelheid ten opzichte van elkaar, dus er is een corresponderende snelheid-tijddilatatie. Wanneer de miniklokken opnieuw tezamen zijn is er geen verschil in de hoeveelheid eigentijd die is verstreken.
Niet-symmetrische snelheid-gerelateerde tijddilatatie
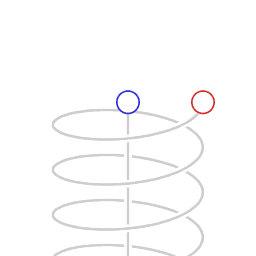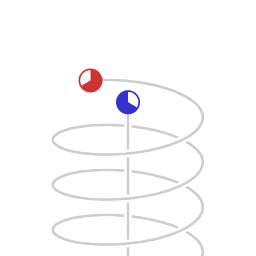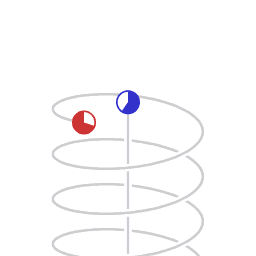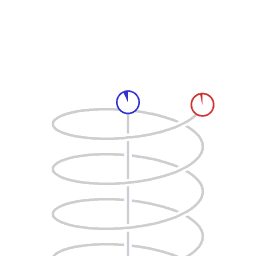
Een rechte wereldlijn en een helix-vormige wereldlijn.
Schematische weergave van asymmetrische snelheid-gerelateerde tijddilatatie. De animatie geeft beweging weer zoals afgebeeld in een Minkowski ruimtetijd-diagram met twee dimensies van ruimte, (het horizontale vlak) en positie in de tijd verticaal. De cirkels beelden klokken uit, die het verstrijken van eigen-tijd tellen. Het Minkowski coördinaten-system beweegt mee met de niet-versnellende klok.
De klok in cirkelvormige beweging telt een kleinere hoeveelheid eigen-tijd dan de niet versnellende klok. In deze animatie is het verschil in de hoeveelheid eigen-tijd die verstrijkt 9n een verhouding van 1:2, en dat correspondeert met een zijwaartse snelheid van 0.866 keer de snelheid van het licht.
Licht dat is uitgezonden door de niet-versnellende klok en ontvangen wordt door de cirkelende klok wordt ontvangen als een blauw-verschoven signaal, in een verhouding van 1:2 . Licht dat is uitgezonden door de cirkelende klok en ontvangen wordt door de niet-versnellende klok wordt ontvangen als een rood-verschoven signaal, in een verhouding van 2:1 .
In deze situatie is de symmetrie verbroken, en overeenkomstig daarmee is er een verschil in de hoeveelheid eigen-tijd die verstrijkt.

Tekst, afbeeldingen en animaties zijn beschikbaar gesteld voor anderen onder de volgende voorwaarden:
Creative Commons Attribution-ShareAlike 3.0 Unported License.
Laatste keer dat deze pagina is bewerkt: 18 juni 2017.