Inertiaaloscillaties
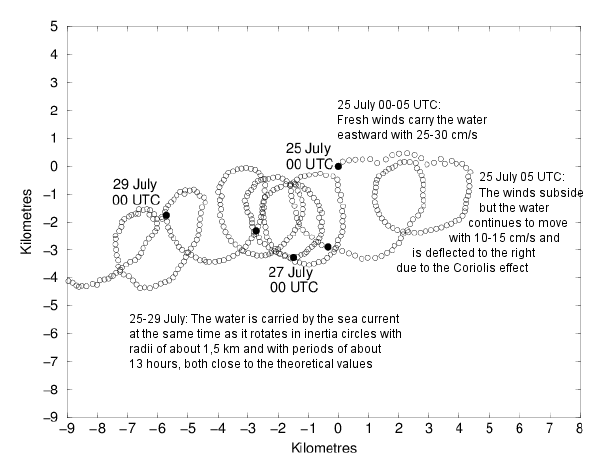
Een vrij drijvende boei in de baltische zee in juli 1969. De bovenste laag water wordt in beweging gezet door sterke westwaartse winden. Wanneer de wind weer is afgezwakt gaat de in beweging gebrachtte waterlaag door in inertiecirkels, als gevolg van het Coriolis effect. Vrij drijvende boeien bewegen mee. Als er tevens constante stroming in het spel is zullen de trajecten cycloiden worden.
De inertaaloscillaties zijn geen kolken, een groep boeien dicht blij elkaar zou gezamelijk bewegen, en niet om elkaar heen draaien.
Ronddraaiende planeet
Het bewegingspatroon van de boei die wordt gevolgd komt door een dynamische situatie die speelt in het geval van een planeet die om zijn as draait. Verderop in dit article een animatie die dit dynamisch patroon illustreert.
Eenvoudiger geval als fysisch model: paraboolvormige schotel.
De dynamiek van inertiaaloscillaties kan worden begrepen door de parallelen met een eenvoudiger geval op te merken: bewegng over het oppervlak van een schaal met paraboolvormige doorsnede.
In het vloeistofdynamiek laboratorium van het MIT Earth, Atmosphere and Planetary sciences faculty kunnen studenten diverse demonstraties opstellen, en één daarvan is het construeren van een parabolische draaitafel. Een platform met een doorsnede van één meter, met een paar centimeter hoge rand, ronddraaient met een hoeksnelheid van 10 omwentelingen per minuut, wordt gevuld met een hars die er enkele uren over doet om uit te harden. Als gevolg van het ronddraaien van het platform zal de hars een zodanige verdeling over het platform bereiken dat in de uiteindelijke toestand het oppervlak een paraboolvorm heeft. De evenwichtstoestand van de ronddraaiende vloeistof wordt 'vast lichaam rotatie' genoemd.. De formele naam van de de vaste vorm die ontstaat is 'omwentelingsparaboloide'.
Voor demonstraties word er een klein schijfje droog ijs op de parabolische schotel geplaatst. De verdampende koolidoxide vormt een dun laagje gas, waardoor er maar heel weinig wrijving is. De hellingshoek van het oppervlak van de schotel is evenredig met de afstand r tot de centrale as. Een puck die met zeer weinig wrijving over het oppervlak kan glijden zal (bij goede benadering) het traject volgend dat aan de linkerzijde van animatie 2 wordt getoond. De vorm van het traject is bij goede benadering een ellips. Omdat de schotel relative langzaam ronddraait (10 omwentelingen per minuut) is hij heel ondiep, het midden is ongeveer een centimeter lager dan aan de rand. Hoe ondieper de parabolische schotel, hoe dichter de feitelijke beweging zal zitten op een zuivere ellips. De MIT draaiende schotel demonstratie toont een afbeelding.
De beweging langs een ellipsvormig traject kan worden gezien als een lineaire combinatie van twee harmonische trillingen (loodrecht op elkaar.)
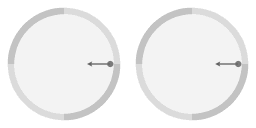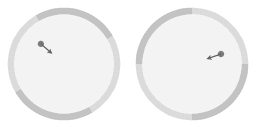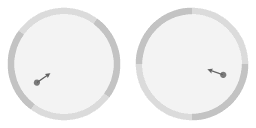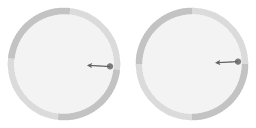
Wrijvingsloze beweging over het oppervlak van een parabolische schotel. De pijl geeft de centripetale kracht weer die er is als gevolg van de hellingshoek van het oppervlak.
De linkerkant van animatie 2 geeft de beweging weer gezien vanuit een niet-draaiend standpunt. De rechterkant geeft de beweging weer zoals gezien vanuit een mee-draaiend standpunt. Om zo min mogelijk wrijving te hebben draaid de schotel rond met dezelfde hoeksnelheid als bij toen hij werkt gemaakt.
De volgende parametrische vergelijking van de positie als functie van tijd beschrijft de beweging van de puck over het oppervlak van de schotel.:
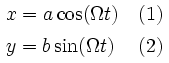
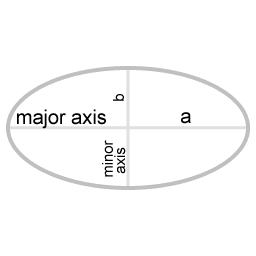
| a | de helft van de lengte van de 'major axis' |
| b | de helft van de lengte van de 'minor axis' |
| ω | 360° gedeeld door de tijdsduur van één omwenteling |
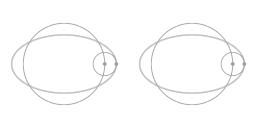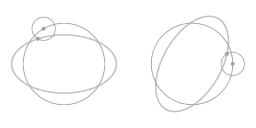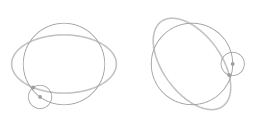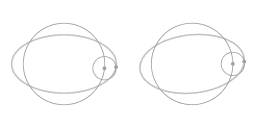
De parametrische vergelijking geeft een complete beschrijving: ze beschrijft de vorm van de baan en de snelheid op ieder punt in de tijd. Er is zowel een oscillatie in de afstand tot de centrale rotatie-as en een oscillatie van de hoeksnelheid.
De parametrische vergelijking kan in twee componenten worden herschikt:
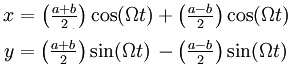
Animatie 4 toont een geometrische weergave van deze herschikking. Het traject over het oppervlak van een parabolische schotel kan worden gezien als een vector combinatie van een uniforme hoeksnelheid lang een grote concentrische cirkel en een uniforme hoeksnelheid langs een epi-cirkel. De epicirkel correspondeert met de eccentriciteit van algemene beweging. Als de beweging langs diet ellipsvormige traject wordt afgebeeld in een draaiend coördinatensysteem komt de eccentriciteit van het ellipsvormge traject naar voren als een beweging langs een kleine cirkel. De animatie toont dat iedere volledige cyclus van het ellipstvormige traject correspondeert met twee cycli van de beweging langs de kleine cirkel.
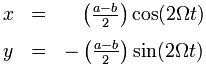
In deze bespreking wordt de taak van coördinatentransformatie gescheiden van het bespreken van de fysica. In dit artikel worden de coördinatentransformatiies verzorgt door de animaties.
Energieomzettingen
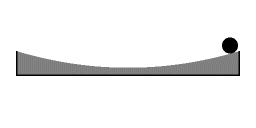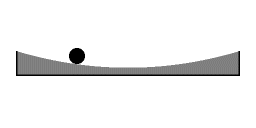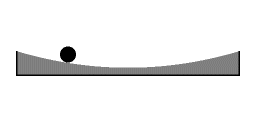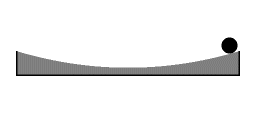
Harmonische oscillatie: de terugdrijvende kracht is evenredig met de afstand tot het midden
Het geval van inertiaaloscillatie op het oppervlak van een parabolische schotel is volledig analoog met het geval van rotatie-vibratie koppeling dat is besproken in het vorige artikel. In het geval van inertiaaloscillatie bereikt de potentiële energie zijn maximum bij de uiterste punten. Naarmate de puck dichter naar de centrale rotatie-as wordt getrokken verricht de centripetale kracht werk, waarbj potentiële energie in kinetische energie wordt omgezet. De kinetische energie is op zijn grootst op de punten waar de puck zich het dichtste bij de centrale rotatie-as bevindt. Wanneer de puck weer bij de centrale rotatie-as vandaan beweegt verricht de centripetale kracht negatieve arbeid; de kinetische energie van het object wordt verminderd.

Uiteindelijke situatie nadat wrijving de energie die was geassociëerd met de eccentriciteit van het bewegingstraject heeft is gedissipeerd.
Een kleine zijstap: een interessant verschil is te zien wanneer dissipatie van energie wordt gevolgd. We nemen aan dat de enige manier om energie te dissiperen bestaat uit wrijving tussen het oppervlak van de parabolische schotel en het voorwerp erop. Eerder was al genoemd dat de schotel ronddraait om wrijving tot een minimum te beperken. (Om de wrijving voor de puck tot een minimum te beperken moet de schotel uiteraard ronddraaien met exact dezelfde hoeksnelheid als toen hij werd gemaakt.) In het geval van inertiaaloscillaties is er dissipatie van energie zolang er een snelheid is ten opzichte van de roterende parabolische schotel. Wrijvng tusssen het oppervlak en de puck verminderd de eccentriciteit van de baan. Wanneer de baan volledig cirkelvormig is geworden is er nog steeds een hoop potentiële en kinetische energie, maar die energie dissipeert niet omdat er geen wrijving is.
Analogie tussen parabolische schotel en platte sferoide
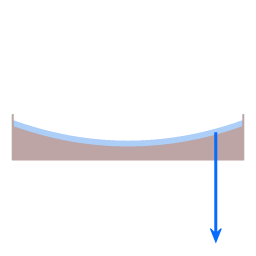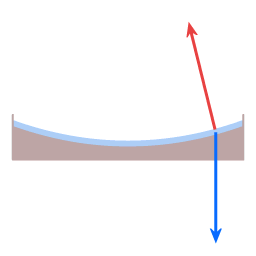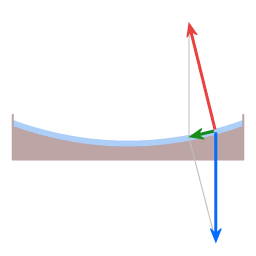
De blauwe pijl geeft de zwaartekracht weer. De rode pijl geeft de normaalkracht weer. De groene pijl geeft de resultante kracht weer.
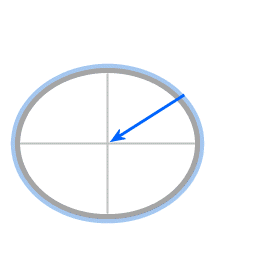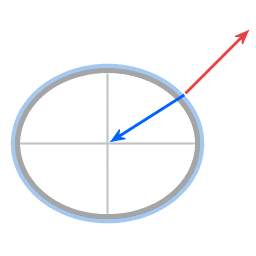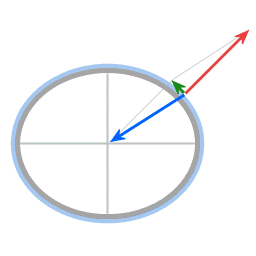
Krachten in het geval van een afgeplatte sferoide. De component van de resultante kracht die parallel aan het oppervlak loopt wordt de poolgerichte kracht genoemd.
Er is een directe analogie tussen de fysica die de vorm van de Aarde bepaald en de fysica die de vorm van een parabolische schotel bepaald.
De solide Aarde is kneedbaar, en de vorm van de Aarde ontwikkelt zich automatisch in de richting van een evenwichtstoestand. Vanwege de draaing om zijn as is de Aarde een afgeplatte sferoide, en niet bolvormig.
Afbeeldingen 7 en 8 tonen de analogie tussen krachten die spelen in het geval van beweging over het oppervlak van een parabolische schotel enerzijds, en in het geval van beweging over het oppervlak van een afgeplatte sferoide anderzijds. De richting van de zwaartekracht en de richting van de normaalkracht wijzen over het algemeen niet exact in dezelfde richting, waardoor er dus een resultante kracht is.
De resultante kracht van zwaartekracht en normaalkracht levert de benodigde centripetale kracht om voorwerpen in cirkelbeweging rondom de aardas te laten lopen. De aanwezigheid van deze resultante kracht geeft aanleiding tot twee effecten: het Eötvös effect en het Coriolis effect (het Coriolis effect zoals dat in meteorologie en oceanografie in rekening wordt genomen.).
Drijfvermogen
Deze centripetale kracht is dan en slechts dan van toepassing als het voorwerp waar het om gaat door de Aarde gedragen wordt. De centripetale kracht is alleen van toepassing als er op het voorwerp een normaalkracht wordt uitgeoefend die de afstand van het voorwerp tot het centrum van de Aarde constant houdt. Dat houdt bijvoorbeeld in dat er in het geval van een hovercraft die zweeft op zijn luchtkussen een centripetale kracht is. Een luchtschip (ook wel bekend als zeppelin) heeft drijfvermogen, en is dus onderhevig aan de centripetale kracht. Het is verleidelijk om te denken dat een luchtschip helemaal vrij is van de grond en daarom helemaal vrij is van zwaartekracht. Maar het luchtschip wordt opgetild omdat de romp ervan groot volume aan lucht wegduwt. Een luchtschip heeft zoveel drijfvermogen als het gewicht van het volume lucht dat door de romp weg wordt geduwd.
In contrast met voorwerpen die drijvende zijn: ieder object dat in vrije val is ondervindt geen normaalkracht, en ondervindt dus niet een centripetale kracht. Bijvoorbeeld, een ballistische raket beweegt langs een kepleriaanse baan (luchtwrijving niet meegerekend) en daarom is er bij een ballistische raket geen centripetale kracht. (Op deze plek wordt met 'centripetale kracht' bedoeld: resultante kracht van zwaartekracht en normaalkracht.) Op een ballistische raket werkt natuurlijk wel de zwaartekracht, maar er is niet nog een kracht die er op werkt. Het volgende artikel Vergelijking van ballistiek en inertiaaloscillaties. is gewijd aan het bespreken van dit verschil.

De poolwaartse kracht.
In meteorologie wordt de poolwaartse kracht in rekening genomen omdat luchtmassa onderhevig is aan de poolwaartse kracht.
Bij goede eerste benadering is het zo dat luchtmassa wrijvingsloos beweegt, en dat die beweging parallel is aan het plaatselijke oppervlak. (Preciezer: parallel aan de plaatselijke geopotentiaalvlakken. Daarom is de kracht die voor luchtmassa relevant is de component van de centripetale kracht parallel aan het plaatselijke oppervlak: de poolwaartse kracht. Om de poolwaartse kracht te berekenen wordt de centripetale kracht vermenigvuldigd met de sinus van de breedtegraad.
Inertiaaloscillatie over het oppervlak van een afgeplatte sferoïde

Inertiaaloscillatie over het oppervlak van een afgeplatte sferoïde.
Animatie 10 geeft de beweging weer van een vrij drijvende boei die meebeweegt met een massa zeewater die in inertiaaloscillatie-beweging is, de beweging die is weergegeven in de afbeelding aan het begin van het artikel.
Deze animatie toont het fenomeen inertiaaloscillatie in een zeer geschematiseerde vorm. Feitelijke inertiaaloscillaties van oppervlakte-zeewater hebben amplitudes in de orde van enkele kilometers, in de animatie hebben de oscillaties een amplitude die een aanzienlijke fractie van de aard-diameter zijn.
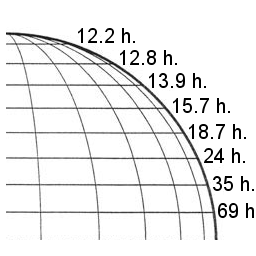
De theoretisch verwachtte periode van inertiaaloscillateis op verschillende breedtegraden
De cyclustijd van een inertiaaloscillatie is verschillend op verschillende breedtegraden. Vlak bij de polen is de cyclustijd 12 uur. Op 30 graden noorderbreedte is de periode van een inertiaaloscillatie 24 uur, en hoe dichter bij de evenaar, hoe langer de periode.
Waarom de oscillaties inertiaaloscillaties worden genoemd

Inertiaaloscillatie over het oppervlak van een afgeplatte sferoïde.
Normaal gesproken is het begrip inertiaalbeweging geassociëerd met uniforme beweging langs een rechte lijn, en de beweging die is afgebeeld in de animatie is verre van uniform; het is niet langs een rechte lijn, en de snelheid is niet constant. Het kenmerk van inertiaalbeweging isd at een versnellingsmeter geen versnelling registreert. In het geval van een boei of een weerballon die meebewegen met inertiaaloscillate zal een interne versnellingsmeter geen versnelling registreren in de richting parallel aan het oppervlak. Natuurlijk zal de versnellingsmeter de zwaartekrachtversnelling meten die loodrecht op het plaatselijke oppervlak werkt, maar het zal de versnelling parallel aan het oppervlak niet registreren omdat versnelling onder invloed van zwaartekracht niet door een versnellingsmeter wordt geregistreerd.
Vergelijking van ballistische beweging en inertiaaloscillaties.

Tekst, afbeeldingen en animaties zijn beschikbaar gesteld voor anderen onder de volgende voorwaarden:
Creative Commons Attribution-ShareAlike 3.0 Unported License.
Laatste keer dat deze pagina is bewerkt: 18 juni 2017.