Rotatie-vibratie koppeling
Twee gewichten die onderling zijn verbonden door een spiraalveer. Er is een rotatie om het gemeenschappelijk massamiddelpunt, en een daarmee gekoppelde oscillatie in de afstand tot het middelpunt en de hoeksnelheid.
Rotatie-vibratiekoppeling treed op als de rotatie-frequentie van een voorwerp nabij of identiek is aan een natuurlijke interne vibratie-frequentie. Animatie 1 toont een eenvoudig voorbeeld. De beweging die in de animatie is afgebeeld is voor de geidealiseerde situatie dat de kracht die door de spriaalveer wordt uitgeoefend lineair toeneemt met de afstand tot het middelpunt van de rotatie. Ook is invloed van wrijving niet meenenomen.
Bij rotatie-vibratie koppeling is er een oscillatie van de hoeksnelheid. Wanneer de spiraalveer de gewichten dichter naar het middelpunt van draaiing trekt verricht de spiraalveer arbeid, en opgeslagen veer-energie wordt omgezet in kinetische energie van de gewichten.
In dit geval, met het om elkaar heen draaien van de gewichten, kan de samentrekkende kracht van de veer de gewichten niet helemaal naar het middelpunt van rotatie trekken. Niet alleen wordt de samentrekkende kracht steeds zwakker naarmate de veer korter is, maar belangrijker, dichter bij het middelpunt van rotatie is de hoeksnelheid zo groot geworden dat de gewichten als het ware weer doorschieten. De afstand van de gewichten tot het middelpunt van rotatie neemt weer toe, er wordt weer veer-energie opgebouwd in de spiraalveer.
Bij het ontwerpen van helicopters moeten er trillingsdemping worden ingebouwd, omdat bij specifieke hoeksnelheden vibraties van de helicopterwieken versterkt kunnen worden door rotatie-vibratie-koppeling. Zonder de demping kunnen de vibraties zo sterk worden dat de wieken afbreken.
In moleculaire fysica is het bekend dat er een koppeling kan zijn van rotatie- en vibratie-energieniveau's. In moleculaire fysica wordt rotatie-vibratie koppeling ook wel rovibronische koppeling en coriolis koppeling genoemd.
Energieomzettingen bij rotatie-vibratie koppeling
De beweging van animatie 1 afgebeeld in een coordinatensysteem dat draait met een constante hoeksnelheid.
Harmonische oscillatie: de terugdrijvende kracht is evenredig met de afstand tot het middelpunt.
Animatie 2 haalt de oscillatie in de hoeksnelheid naar voren. Er is een nauwe analogie met harmonische trilling.
Op het moment dat een harmonische oscillatie zich op zijn middelpunt bevindt is alle energie van het systeem kinetische energie. Op de punt het verst van het middelpunt vandaan is alle energie van het systeem potentiële energie. De energie van het systeem zit in een heen-en-weer cyclus van kinetische energie en potentiëlen energie.
In vergelijkbare zin is het zo dat er in het geval van de beweging die is afgebeeldt in de animatie er een heen-en-weer cyclus is van kinetische energie en potentiële energie. Op het moment van maximale uitrekking van de veer is de potentiële energie op zijn hoogst, op het moment van maximale hoeksnelheid is de kinetische energie op zijn grootst.
(In het geval van een echte veer is er ook de factor wrijving. Met een echte veer zal de trilling gedempt worden en de uiteindelijke situatie zal zijn dat de massa's om elkaar heen draaien met een constante onderlinge afstand, met dus een constante spanning van de veer. In de uiteindelijke situatie staan de kinetische energie en de potentiële energie in een verhouding van 1:1 ten opzichte van elkaar.Voor een discussie van de rol die wordt gespeeld door impuls, zie opmerking over impuls.
Wiskundige afleiding
Cartesisch coördinatenstelsel
De beweging van de om elkaar heen draaiende gewichten is beweging in een plat vlak, dus twee dimensies van ruimte zijn voldoende om de beweging te beschrijven.
In deze bespreking zijn de volgende vereenvoudigingen toegepast: de veer zelf wordt als massaloos, genomen, en de veer wordt als een ideale veer beschouwd; de aantrekkende kracht neemt lineair toe bij uitrekken van de veer. Met andere woorden: de centripetale kracht is recht evenredig met de afstand tot de centrale as van draaing. Een centripetale kracht met deze eigenschap wordt een harmonische kracht genoemd.
De beweging van de gewichten in twee dimensies kan worden ontbonden in twee harmonische oscillaties, haaks op elkaar.
De volgende parametische vergelijking van de positie als fucnti van tijd beschrijft de beweging van de om elkaar heen draaiende gewichten:
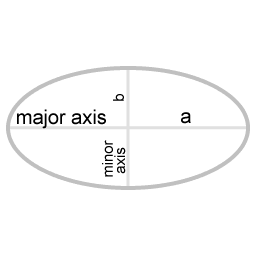
| a | De helft van de lengte van de 'major axis' |
| b | de helft van de lengte van de 'minor axis' |
| ω | 360° gedeeld door de tijdsduur van één omwenteling |
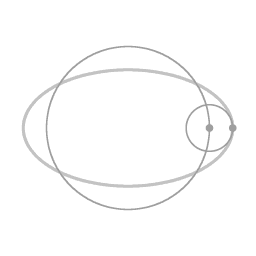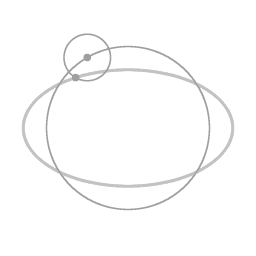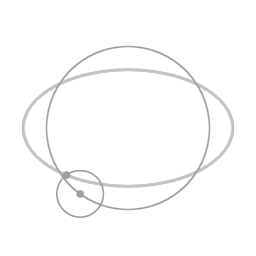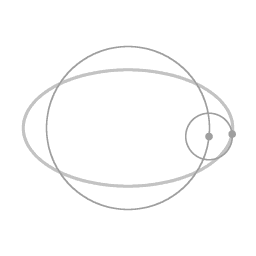
Een ellips-vormige baan kan worden opgevat als een cirkelvormige baan (in dit voorbeeld tegen de klok in, met de excentriciteit als een epi-cirkel (met de klok mee).
De beweging als functie van tijd kan ook worden beschreven als een lineaire combinatie van twee uniforme cirkelvormige bewegingen. De parametrische vergelijkingen (1) en (2) kunnen als volgt herschreven worden:
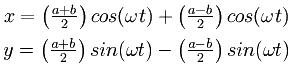
Transformatie naar een roterend coördinatensysteem elimineert de algemene cirkelvormige beweging, en laat de eccentriciteit van de ellips-vormige baan over. Deze eccentriciteit heeft zelf een middelpunt, en dat bevindt zich op een afstand van (a + b) / 2 vanaf de centrale draaingsas.
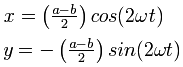
Dat is wat er feitelijk te zien is in Animatie 2, waarin de beweging is afgebeeld in een coördinatensysteem dat draait met een constante hoeksnelheid. Gemeten ten opzichte van het middelpunt van de eccentriciteit heeft de beweging zoals afgebeeld in het draaiende coördinatensysteem een hoeksnelheid van 2ω, tweemaal de hoeksnelheid van de algemene beweging.
De spiraalveer verricht voortdurend arbeid. Preciezer: de spiraalveer oscilleert tussen positieve arbeid verrichten (de kinetische energie van de gewichten vergroten) en negatieve arbeid verrichten (de kinetische energie van de gewichten verkleinen).
Bespreking in termen van vector notatie
Gegeven in deze situatie: de centripetale kracht is een harmonische kracht.
De verzameling an alle oplossingen voor deze bewegingsvergelijking bestaat uit zowel cirkelvormige banen als ellips-vormige banen. Al deze oplossingen hebben dezelfde omlooptijd. Dit is een speciaal kenmerk van beweging onder invloed van een harmonische kracht: de omlooptijd is onafhankelijk van de amplitude van de baan; alle banen hebben dezelfde omlooptijd.
Wanneer de beweging wordt afgebeeld in een draaiend coördinatensysteem worden de centrifugale term en de coriolis term toegevoegd aan de bewegings vergelijking.
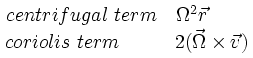
Hier staat Ω voor de hoeksnelheid van het draaiende coördinatensysteem ten opzichte van het inertiaalsysteem. v is de snelheid van het bewegende voorwerp ten opzichte van het draaiende coördinatensysteem. Het volgende is belangrijk: de centrifugale term heeft alleen betrekking op het coördinatensysteem, de centrifugale term staat los van de beweging van het voorwerp. De hoeksnelheid van het bewegende voorwerp is onderhevig aan verandering, maar de Ω in de centrifugale term is dat niet: het is de uniforme hoeksnelheid van het draaiende coördinatensysteem.
Het is verleidelijk om de centrifugale term te interpreteren als de versnelling die een versnellingsmeter zal meten. Het is ook wel zo dat als de beweging perfect cirkelvormig is de centrifugale term overeenkomt met hoeveel G's er worden getrokken, maar die overeenkomst gaat niet op wanneer de beweging niet perfect cirkelvormig is.
Om het werken met de formules te versnellen worden de centrifugale term en de coriolis term onder voorbehoud als krachten gerekend. Dat geeft alles bij elkaar de volgende drie termen in de bewegingsverglijking voor beweging ten opzichte van een coördinatensysteem dat draait met hoeksnelheid Ω.
Zowel de centripetale kracht als de centrifugale term in de bewegingsvergelijking zijn evenredig met r. De hoeksnelheid van het draaiende coördinatensysteem is afgestemd op de omlooptijd van het voorwerp dat beweegt langs een ellipsvormige baan. Daarom zijn de vector van de centripetale kracht en de vector van de centrifugale term op alle afstanden tot het centrum even groot en in tegenovergestelde richting, en vallen ze in de bewegingsvergelijking weg tegen elkaar.
Dit tegen elkaar wegvallen in de bewegingsvergelijking is alleen van toepassing als de centripetale kracht een harmonische kracht is.
In dit voorbeeld is de enige overgebleven term in de bewegingsvergelijking de coriolis term.
Deze overgebleven term staat nu voor iets waar de oorspronkelijke coriolis term niet voor stond. De overgebleven term staat nu voor de effecten van de centripetale kracht, maar dan afgebeeld in een draaiend coördinatensysteem. De factor 2 van het Coriolis effect correspondeert met het feit dat voor iedere cyclus van de algemene beweging de de eccentriciteit in de ellipsvormige baan twee keer zijn cyclus doorloopt.
Coriolis effect
Het is terecht om de beweging ten opzichte van het draaiende coördinatensysteem te zien als het simpelste en puurste voorbeeld van het Coriolis effect.
Zoals te verwachten was heeft de analyse met behulp van vector-notatie de vorige analyse bevestigd. De spiraalveer verrricht voortdurend arbeid. Preciezer: de spiraalveer oscilleert tussen positieve arbeit verrichten (de kinetische energie van de gewichten vergroten) en negatieve arbeid verrichten (de kinetische energie van de gewichten verkleinen).
Opmerking over impuls
In de sectie 'Energieomzettingen bij rotatie-vibratie koppeling' wordt er niet gekeken naar impuls, maar wordt de dynamica gevolgd door te kijken naar de energieomzettingen. Het voordeel van het volgen van de energie-omzettingen is dat dan wordt gekeken naar oorzaak-gevolg relatie.
De wetmatigheid van behoud van impuls is een wetmatigheid van symmetrie van bewegingswetten in de ruimte, en niet een wetmatigheid van oorzaak en gevolg. Een illustratie daarvan is het voorbeeld van een kanon dat wordt afgevuurd. Wanneer een kanon wordt afgevuurd zal het projectiel uit de loop schieten naar het doel, en de loop zal terugslag vertonen. Het zou een fout zijn om te beweren dat het projectiel de loop met hoge snelheid verlaat vanwege de terugslag van de loop. Er is natuurlijk altijd terugslag van de loop (de wetmatigheid van behoud van impuls), maar dat is niet de oorzaak. Het oorzakelijke mechanisme zit in de energie-omzettingen: de explosie van het kruit zet potentiële chemische energie om in de potentiële energie van een dicht samengeperst gas. Het expanderende gas oefent een kracht uit op zowel het projectiel als het inwendige van de loop. Door de werking van die kracht wordt potentiële omgezet in kinetische energie van zowel projectiel als loop.
Vergelijkenderwijs: in het geval van rotatie-vibratie koppeling is de toename van hoeksnelheid bij samentrekking in overeenkomst met het principle van behoud van impulsmoment, maar dat moet niet worden verward met behoud van impulsmoment als de oorzaak. In het geval van rotatie-vibratie koppeling is de oorzaak de kracht die wordt uitgeoefend door de spiraalveer.
(terug naar het artikel)
Inertiaaloscillaties
Grote delen van dit artikel zijn in engelstalige vorm door mij geupload naar het wikipedia artikel over Rotational-vibrational coupling.
Wikipeda text is available under the terms of the GNU Free Documentation License

Tekst, afbeeldingen en animaties zijn beschikbaar gesteld voor anderen onder de volgende voorwaarden:
Creative Commons Attribution-ShareAlike 3.0 Unported License.
Laatste keer dat deze pagina is bewerkt: 18 juni 2017.