Behoud van impulsmoment
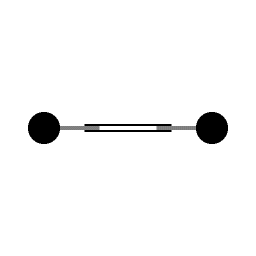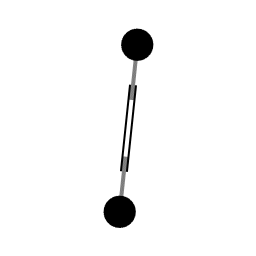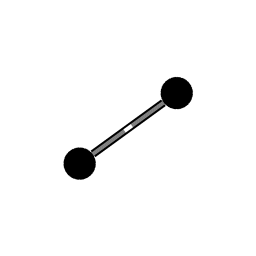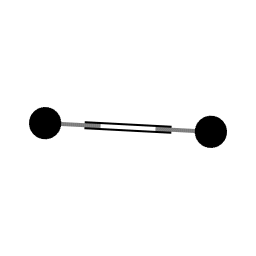
Twee gewichten die verbonden zijn met zuigers. Hydraulisch mechaniek (niet afgebeeld) trekt de gewichten dichter naar het middelpunt van rotatie. Het samentrekken zorgt voor versnelling van de hoeksnelheid.
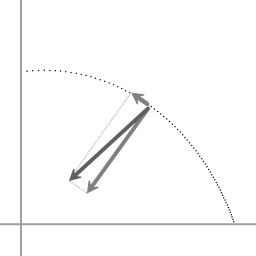
Typerend traject tijdens samentrekking. De middelpuntgerichte kracht kan worden ontbonden in een haakse en een paralelle component.
Inleiding
De algemene reikwijdte van impulsmoment omvat verschijnselen die misschien nauwelijks verwant lijken: het impulsmoment dat betrokken is bij omlopende beweging zoals planeetbanen, en het impulsmoment van een vast voorwerp dat om zijn eigen as aan het draaien is. Vele leerboeken bespreken alleen het impulsmoment van een vast voorwerp. In dit artikel zal ik mij concentreren op omlopende beweging.
Bij impulsmoment gaat het om twee of meer voorwerpen die een kracht op elkaar uitoefenen. (In het geval van impulsmoment van een vast voorwerp oefent de bindingskracht van het materiaal de benodigde kracht uit. Als een voorwerp sneller om zijn as draait dan de bindingskracht aankan, dan zal het voorwerp uiteenspatten.)
Animatie 1 is er op gericht om te laten zien hoe impulsmoment een rol speelt in omlopende beweging. Wanneer een draaiend geheel samentrekt dan neemt de hoeksnelheid toe. Omgekeerd, als de afstand tot het middelpunt van rotatie toeneemt gaat de hoeksnelheid naar beneden.
Ontbinden
Afbeelding 2 illustreert de mechanica tijdens de samentrekkende fase. De donkerste pijl, degene die naar het nulpunt van het coordinatensysteem wijst, staat voor de centripetale kracht. Er is een belangrijk verschil met cirkelvormige beweging. Bij cirkelvormige beweging werkt de centripetale kracht precies in een hoek van 90 graden op de richting van de snelheid, en dan is het enige dat de centripetale kracht doet het veranderen van de richting van de snelheid. Maar tijdens de samentrekking is de snelheid van de gewichten niet haaks op de centripetale kracht, en dan kan die centripetale kracht worden opgevat als ontbonden in twee componenten: een component haaks op de snelheid op dat ogenblik, en een component evenwijdig aan de snelheid op dat ogenblik. De evenwijdige component maakt dat snelheid van het gewicht toeneemt.
Wat we graag willen weten is hoeveel hoekversnelling er is als gevolg van de samentrekking.
Geschiedenis
Een essentiële aanwijzing voor de oplossing van dat probleem was al opgemerkt voordat Newtoniaanse dynamica was geformuleerd. Eén van de wetten van planeetbeweging die Kepler had gevonden was de perkenwet: in hun baan om de Zon bestrijken de planeetbanene in gelijke tijdintervallen gelijke oppervlaktes. Voor Kepler was de perkenwet een empirische wetmatigheid; met behulp van de perkenwet kon hij de banen van al de planeten beschrijven, maar Kepler kon niet weten of de perkenwet een aparte wetmatigheid was, of dat ze deel uitmaakte van een veelomvattender geheel van bewegingswetten. Newton liet zien dat het laatste het geval is.
De eerste stelling in Newtons Principia is de perkenwet. Om precies te zijn, Newton leidde een meer algemene vorm van de perkenwet af, de afleiding die Newton gaf is niet alleen geldig voor de zwaartekracht die hemellichamen op elkaar uitoefenen, maar voor iedere centrale kracht. Ik zal deze veralgemeniseerde vorm 'Newton's perkenwet' noemen.
Ik zal eerst Newton's afleiding geven, en dan zal ik laten zien hoe Newon's perkenwet en de wet van behoud van impulsmoment verbonden zijn.

Twee voorwerpen, R en T, die met constante impuls bewegen. De impuls van hun gemeenschappelijk massamiddelpunt is daarmee ook constant.
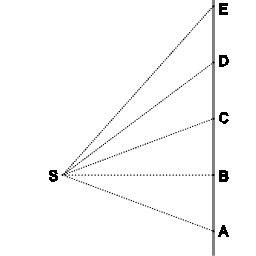
De perkenwet in het geval van uniforme snelheid.
Afleiding van de perkenwet
Newtons afleiding gaat terug op de volgende elementen:
| · | Het principe van behoud van lineaire snelheid (de eerste wet van Newton). |
| · | De regels van het optellen van snelheden. |
| · | Behoud van impuls wanneer twee voorwerpen een kracht op elkaar uitoefenen. |
| · | Symmetrie van de natuurkundige wetten voor alle richtingen in de ruimte. |
De wet van behoud van lineaire snelheid kan zo worden geformuleerd dat ze zich speciaal ervoor leent om ingezet te worden in de afleiding van de perkenwet.
Als er geen kracht wordt uitgeoefend (of als de krachten tegen elkaar wegvallen) dan zal een voorwerp in gelijke tijdintervallen gelijke afstanden afleggen.
In afbeelding 4 staat de dikke lijn voor de wet van behoud van lineaire snelheid. Een voorwerp beweegt langs de punten A, B, C, D, E, waarbij in gelijke tijdintervallen gelijke afstanden worden afgelegd. Neem als punt S het massamiddelpunt van twee voorwerpen, R and T (zoals getoond in afbeelding 3). De stippellijnen geven driehoeken aan. Het is duidelijk dat SAB, SBC, SCD and SDE allemaal dezelfde oppervlakte hebben: gelijke oppervlakken worden bestreken in gelijke tijdintervallen. Hier blijkt dat behoud van lineaire snelheid en de perkenwet onderling verband houden. Wanneer er geen kracht werkt dan zijn behoud van lineaire snelheid en de perkenwet hetzelfde principe.
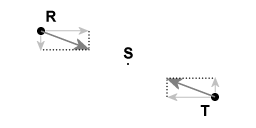
De voorwerpen R en T oefenen een kracht op elkaar uit. De impuls van hun gemeenschappelijk massamiddelpunt is behouden.
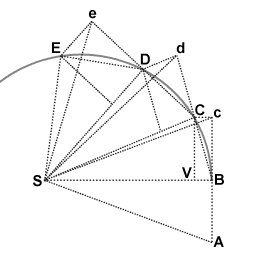
Meetkundige demonstratie hoe de perkenwet volgt uit de bewegingswetten.
Afbeelding 5 benadrukt de eigenschap van punt S, het gemeenschappelijk massamiddelpunt, dat als voorwerp R en voorwerp T een kracht op elkaar uitoefenen de impuls van het gemeenschappelijk massamiddelpunt behouden blijft.
Afbeelding 6 toont Newton's meetkundige demonstratie van de perkenwet. Het diagram is een iets aangepaste versie van het diagram dat Newton in de Principia gaf; wiskundig is het hetzelfde.
Voorwerp T (niet getekend in afbeelding 6) beweegt langs het gekromde traject dat langs de punten A, B, C, D and E gaat. De kracht die voorwerp T ondervindt veroorzaakt verandering van snelheid. Voor de afleiding wordt de gelijkmatige verandering van snelheid benadert met onmiddelijke veranderingen van snelheid die plaatsvinden op korte gelijke tijdintervallen na elkaar. Hoe kleiner je de tijdintervallen neemt hoe meer de opeenvolging van onmiddelijke snelheidsveranderingen een benadering is van gelijkmatige snelheidverandering.
Punt S is het gemeenschappelijk massamiddelpunt van de voorwerpen R and T. Voorwerpen R en T oefenen een kracht op elkaar uit. De kracht die de voorwerpen R en T op elkaar uitoefenen is wederzijds: dat maakt dat de bewegingstaat van punt S inertiale beweging is. Voor deze afleiding van de perkenwet is het voldoende dat punt S in een staat van inertiaalbeweging is, en dat de kracht die op voorwerp T wordt uitgeoefend ten allen tijde is gericht op punt S.
Op punt B ontvangt voorwerp T een stoot richting punt S, waardoor de beweging een snelheidscomponent richting punt S krijgt. Als voorwerp T die stoot niet zou hebben gekregen zou het zijn doorgegaan naar punt c (in een gelijke hoeveelheid tijd).
De daadwerkelijke verplaatsing BC is de optelsom van de verplaatsingen Bc en BV. Het gaat hier feitelijk om optellen van twee snelheidsvectoren die niet in dezelfde richting wijzen. Het resultaat van de optelling wordt hier meetkundig gevonden: het is de diagonaal van de vierhoek.
De driehoeken SAB en SBc hebben dezelfde oppervlakte. Omdat de lijnen SB en Cc parallel zijn hebben de driehoeken SBc en SBC dezelfde oppervlakte. Daaruit volgt dat de driehoeken SAB en SBC dezelfde oppervlakte hebben.
De punten B, C en d liggen op dezelfde lijn. Als object T geen stoot zou ontvangen op punt C dan zal het in een gelijke hoeveelheid tijd doorgaan naar d. Omdat de bewegingswetten hetzelfde zijn voor iedere richting in de ruimte is dezelfde redenatie geldig voor de eropvolgende driehoeken. Daarmee is gedemonstreerd dat de driehoeken SBC, SCD en SDE, die in gelijke tijdintervallen worden bestreken, gelijke oppervlakten hebben.
In de limiet van steeds kleinere tijdintervallen benaderen de lijnstukken BC, CD en DE het gekromde traject steeds dichter.
Principes
Het is interessant om te zien hoe de inhoud van de afleiding een licht werpt op de natuurkundige wetmatigheid die ze bewijst. Bij de elementen van de meetkundige afleiding zit de wet van samenstelling van snelheden: snelheidsvectoren worden opgeteld volgens de stelling van Pythagoras. Er zijn vele manieren om de stelling van Pythagoras te bewijzen, ik vind de bewijzen die werken met behoud van oppervlakte zeer aansprekend. Bijvoorbeeld de volgende wikipedia animatie. Dit zegt iets over hoe de wetten van samenstelling van snelheden en de perkenwet onderling gerelateerd zijn.
Impulsmoment
Tot dusverre heb ik de natuurkunde in meetkundige termen besproken. Het doel van de volgende bespreking is om een algebraïsche uitdrukking voor de behouden grootheid te verkrijgen.
De oppervlakte van een driehoek is evenredig met het produkt van de basis en de hoogte. In dit geval is de basis van de driehoek r, de radiale afstand, en de hoogte is r·Δθ (waarbij Δθ de hoek is die bestreken wordt in het tijdinterval Δt)
De oppervlakte delen door het tijdinterval geeft de hoeveelheid oppervlak die per eenheid van tijd wordt bestreken.
In de limiet van Δt naar infinitisimaal is de uitdrukking voor de behouden grootheid evenredig met de volgende uitdrukking:
Waarbij ω de hoeksnelheid is.
Dat levert een algebraïsche uitdrukking voor de behouden grootheid: ze is evenredig met r²ω
Daarmee is de vraag die aan het begin is gesteld beantwoord: als een draaiend geheel samentrekt, hoeveel hoekversnelling zal die samentrekking dan veroorzaken? Het antwoord is dat als de radiale afstand is gehalveerd de hoeksnelheid zal zijn verviervoudigd.
Impulsmoment L is gedefiniëerd als het traagheidsmoment vermenigvuldigd met de hoeksnelheided. L = mr²ω. Het voordeel van impulsmoment op die manier definiëren is aansluiting bij het begrip kinetische energie. De kinetische energie van een voorwerp met een snelheid v is ½mv². We kunnen de volgende uitwissling doen: v = ωr, en dat levert een uitdruking voor de kinetische energie die is geasscociëerd met cirkelvormige beweging met de snelheid v: ½mr²ω²
The grootheid mr² wordt het traagheidsmoment genoemd, en het is in de natuurkunde van draaing de tegenhanger van traagheid.
Oorzaak en gevolg

Herhaling van animatie 1. Twee gewichten die zijn verbonden met zuigers. Hydraulisch mechaniek (niet afgebeeld) trekt de gewichten dichter naar het middelpunt van rotatie, waardoor hoekversnelling wordt veroorzaakt.
Impuls gaat over symmetrie in de ruimte van de natuurkundige wetten, en niet zozeer over een oorzaak-naar-gevolg relatie. Dit laat zich illustreren met het voorbeeld van een kanon die wordt afgevuurd. Als een kanon wordt afgevuurd zal het projectiel uit de loop schieten, naar het doelwit toe, en de loop zal een terugslag ondergaan. Het zou fout zijn om te suggereren dat het projectiel de loop met hoge snelheid verlaat vanwege de terugslag van de loop. Het wegschieten van het projectiel en de terugslag van de loop gebeuren tegelijkertijd, en daarom kan het ene niet de oorzaak zijn van het andere.
Het oorzaak-naar-gevolg verband ligt in de voorgaande energieomzettingen: de ontploffing van de springlading zet potentiële chemische energie om in de potentiële energie van een sterk gecomprimeerd, zeer heet gas. Het gas zet uit en verricht arbeid op zowel het projectiel als op kanonloop. Op die manier wordt kinetische energie overgedragen aan zowel projectiel en loop.
De natuurkunde van hoekversnelling door samentrekking is vergelijkbaar daaraan: het is wel zo dat de toename van hoeksnelheid precies wordt beschreven met het principe van behoud van impulsmoment, maar daar moet niet de conclusie aan worden verbonden dat behoud van impulsmoment als oorzaak-naar-gevolg relatie kan gelden. Bij hoekversnelling door samentrekking van een draaiend systeem is de oorzaak de centripetale kracht die arbeid verricht.

Tekst, afbeeldingen en animaties zijn beschikbaar gesteld voor anderen onder de volgende voorwaarden:
Creative Commons Attribution-ShareAlike 3.0 Unported License.
Laatste keer dat deze pagina is bewerkt: 18 juni 2017.