Dit artikel is een introductie van basisbegrippen. Ik maak geen gebruik van wiskunde formules, alleen diagrammen en animaties. In de andere artikelen op deze website worden de beweringen onderbouwd met wiskunde. Hier moet u op mijn woord vertrouwen.

Het Coriolis effect in Meteorologie

Op deze pagina bespreek ik het rotatie-van-de-aarde-effect waar in de meteorologie rekening mee wordt gehouden. Dit wordt het 'Coriolis effect' genoemd. (Het rotatie van de aarde effect dat relevant is voor ballistiek is onderwerp van de volgende twee Java simulaties (engelstalige pagina's): Great circles and Ballistics).

Het feit dat de aarde draait heeft om te beginnnen als effect dat het niet een perfecte bol is; er is uitdijing van de evenaar. Een volledig vloeibare planeet zou dezelfde vorm hebben. De uitdijing is gering; op foto's genomen vanuit de ruimte zie je het er niet aan af, en daardoor kan het lijken alsof het verwaarloosbaar is, en dat is niet het geval. De aardrotatie en de daaruit resulterende evenaar-uitdijing samen geven het effect dat van belang is voor meteorologie.

Een model: parabolische schotel

Beweging over het aardoppervlak is lastig te visualiseren, en daarom stap ik nu over op een model dat eenvoudiger is, maar dat toch de eigenschappen heeft die aanleiding geven voor het Coriolis effect.

Source: PAOC, MIT  met toestemming van John Marshall

De schotel op de afbeelding is in het midden iets dieper dan aan de omtrek. De schotel is als volgt vervaardigd: een platte schijf met een rand draaide rond met een constante hoeksnelheid (10 omwentelingen per minuut), en een kunsthars was erin uitgegoten. Het vloeibare materiaal verdeelde zich over de gehele schijf. De hars had voldoende tijd om een evenwichtstoestand te bereiken voordat het uithardde. De uiteindelijke vorm is een evenwicht tussen de neiging om naar buiten en tegen de rand omhoog te vloeien, en de invloed van de zwaartekracht om het niveau van een vloeistof vlak te maken.
Het oppervlak werd geschuurd om een zeer gladde afwerking te krijgen. De dwarsdoornsede van het aflopende oppervlak is een parabool. (De ronding is te ondiep om het te zien, maar het is een parabool-vorm.)

Verder is er een overhangende constructie. De verticale stang die op de afbeelding te zien is zit niet aan de werktafel bevestigd, maar aan de schotel; als de schotel draait draait de stang mee. Aan de overhangende constructie zit een camera bevestigd, en de beelden van die camera tonen de beweging gezien vanuit een mee-draaiend perspectief.

De parabolische schotel fungeert als volgt als model voor de draaiende aarde: als je water zou uitgieten over de schotel (al ronddraaiend met dezelfde 10 omwentelingen per minuut) dan verdeelt dat water zich op dezelfde manier over de schotel als de kunsthars dat deed. Je krijgt dus een gelijkmatig laagje water.

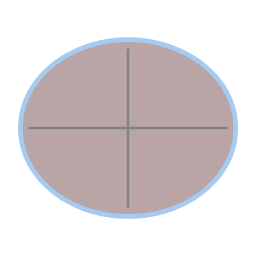
• Van nature is een wateroppervlak plat. Door de draaing gaat het wateroppervlak naar een paraboolvorm.
• Een planeet is van nature bolvormig. Door de draaing ontstaat er een uitdijing aan de evenaar. Het water op de planeet is overal een laag van een paar kilometer dik.

Overigens, de aarde is niet vanuit een bolvorm naar de huidige afgeplatte vorm gegaan. Aan het begin van het zonnestelsel, toen de aarde zich begon te vormen, was het een protoplanetaire schijf. Deze schijf trok zichzelf gaandeweg samen tot een planeet. Omdat de protoplaneet om zijn as draaide ging dat samentrekken niet helemaal door tot een bolvorm.

De parabolische schotel is hol, en de aarde is convex, en het is niet direct duidelijk hoe het één model moet staan voor het ander. De volgende serie afbeeldingen is gemaakt om dat te overbruggen.

A

B

C

D

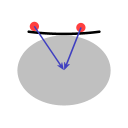
Afbeelding A laat zien dat als een schotel zo groot als een continent op de noordpool geplaatst zou worden de zwaartekracht van de aarde voorwerpen op die schotel naar het midden zou trekken.

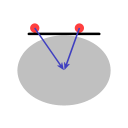
Op afbeelding B wordt een reusachtige platte schijf weergegeven met een rechte lijn. De schijf is plat, maar omdat de zwaartekracht van de aarde naar het middelpunt van de aarde trekt is het toch zo dat voorwerpen op de schijf naar het midden worden getrokken.

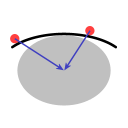
Op afbeelding C is een vorm weergegeven die met de vorige twee voorbeelden gemeenschappelijk heeft dat voorwerpen die erop liggen naar het midden getrokken worden. De vorm is weliswaar convex, maar effectief is het een kom omdat de omtrek, de rand, verder bij het middelpunt van zwaartekrachtaantrekking vandaan is dan het midden.

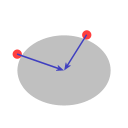
Tenslotte, afbeelding D is een weergave van hoe het werkt voor de aarde, met de uitdijing aan de evenaar. Effectief: ieder halfrond is een kom, en de evenaar is de rand van die kommen.

Kracht

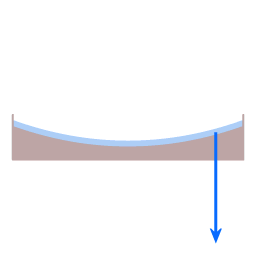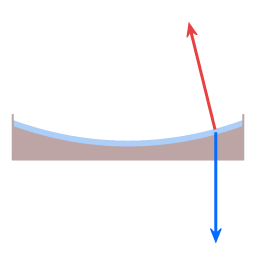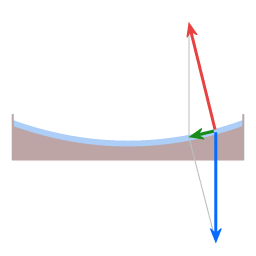
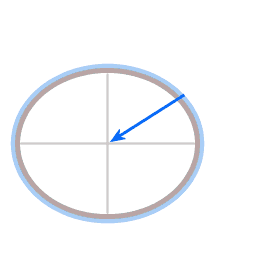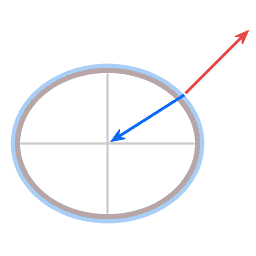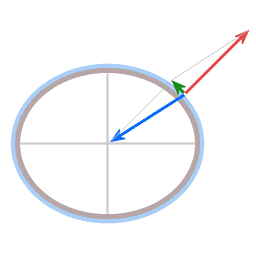
In beide diagrammen is de blauwe pijl een weergave van de zwaartekracht. In het geval van de schotel trekt die recht naar beneden, in het geval van de aarde trekt die naar het aardmiddelpunt. De rode pijl is een weergave van wat de 'normaalkracht' wordt genoemd. (Het woord 'normaal' wordt hier gebruikt in de wiskundige betekenis van 'loodrecht op een oppervlak'.) Het oppervlak van de schotel draagt het water, en dat houdt dus in dat het oppervlak een kracht uitoefent op het water, loodrecht op het oppervlak.
In de gevallen hier is de richting van de normaalkracht niet precies tegenover de richting van de zwaartekracht. De hoek ertussen geeft aanleiding tot een middelpuntgerichte kracht, weergegeven met de groene pijl.

(Voor enkele opmerkingen over hoe groot de uitdijing van de aarde is, en hoe groot de middelpuntgerichte kracht is, zie de uitdijing van de evenaar bespreking op deze pagina.)

Over de parabolische schotel glijden

Bij deze schotel wordt er geen water in gegoten, dat zou te zwaar worden. In plaats daarvan worden voor demonstraties kleine voorwerpen, gemaakt om heel weinig wrijving te hebben, op het oppervlak geplaatst.

In bovenstaande animaties worden twee perspectieven getoond. Links de daadwerkelijke beweging van de schotel, rechts de beweging zoals gezien door de overhangende video-camera. Op de rand van de schijf zijn in grijstinten vier kwadranten aangebracht, om goed te laten zien welk perspectief het niet-draaiende perspectief is.

Het wrijvingsloze voorwerp is op de parabolische schotel geplaatst op zo'n manier dat het met de schotel meedraait. De schotel draait rond met dezelfde hoeksnelheid als toen hij werd vervaardigd. In dat geval is de middelpuntgerichte kracht precies sterk genoeg om cirkelvormige beweging in stand te houden. Als je meerdere voorwerpen op de draaiende schotel zou plaatsen, allemaal zonder snelheid ten opzichte van de schotel, dan zouden ze simpelweg hun posities ten opzichte van elkaar behouden. Als je in dat geval alleen maar het beeld van overhangende camera zou hebben dan is nauwelijks te zien of het gaat om een draaiend geheel of een stilstaand geheel.

Maar als het voorwerp een snelheid heeft ten opzichte van de draaiende schotel gebeuren er interessante dingen.

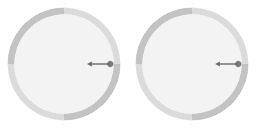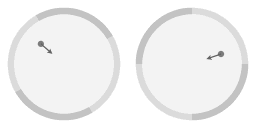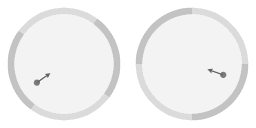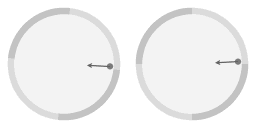
In bovenstaande animaties is er een pijl toegevoegd om te benadrukken dat de helling van het oppervlak aanleiding geeft tot een middelpuntgerichte kracht. En een eigenschap van de parabolische vorm is dat de middelpuntgerichte kracht die komt van de hellingshoek precies evenredig is met de afstand tot de centrale draaingsas. Vanaf hier zal ik 'evenredige kracht' schrijven als verkortte vorm voor 'een kracht die evenredige is met de afstand tot de centrale draaingsas.'

Vergeleken met de cirkelvormige beweging heeft het wrijvingsloze voorwerp een duwtje gekregen; het heeft een snelheid ten opzichte van de paraboolvormige schotel. Merk op dat gemiddeld genomen het voorwerp nog steeds meedraait met de schotel. Het verschil is dat de beweging nu niet cirkelvormig is maar ellips-vormig.

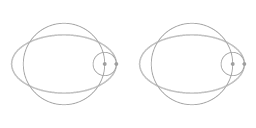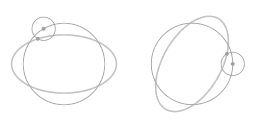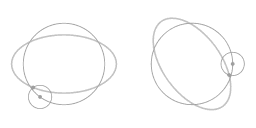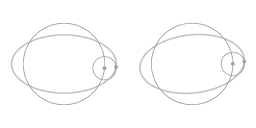
Bovenstaande animatie toont dat de beweging langs het ellips-vormige traject gezien kan worden als een combinatie van twee cirkels: een hoofdcirkel en een epi-cirkel. Gezien vanuit het meedraaiende perspectief zie je de beweging langs de epi-cirkel.

Bewegingregel

De volgende bewering wordt in andere artikelen op deze site bewezen, hier wordt de bewegingsregel zonder meer gesteld:

• Als de kracht die rondlopende beweging in stand houdt een evenredige kracht is, dan is de beweging gezien vanuit meedraaiend perspectief precies de epi-cirkel.

Die bewegingsregel is om de volgende reden belangijk:

• Wanneer het voorwerp langs de epi-cirkel beweegt buigt het de hele tijd af (en in de voorbeelden hier is die afbuiging naar rechts). De epi-cirkel is een perfecte cirkel, en dat houdt in dat de neiging om af te buigen in alle richtingen even sterk is.

Deze bewegingsregel is van toepassing zowel in het geval van beweging over het oppervlak van de parabolische schotel en in het geval van beweging over het aardoppervlak.

Oorzaak van het afbuigen

De oorzaak van het afbuigen is voor iedere richting verschillend, maar de gemeenschappelijke factor is dat het in iedere richting een samenspel is van de middelpuntgerichte kracht en de traagheid van het rondlopende voorwerp.

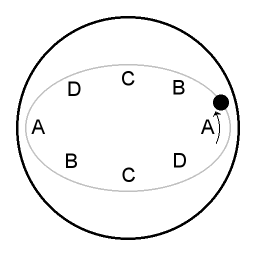
Een overzicht:

A	Bij de delen van de omloop die gelabeld zijn met A is de snelheid van het voorwerp kleiner dan die van de parabolische schotel. Er is dan een overschot aan middelpuntgerichte kracht, en het voorwerp wordt dichter naar de centrale as toe getrokken.
C	Bij de delen van de omloop die gelabeld zijn met C is de snelheid van het voorwerp groter dan die van de parabolische schotel. De middelpuntgerichte kracht is dan niet sterk genoeg, en het voorwerp raakt weer verder verwijderd van de centrale as.
B	Bij de delen van de omloop die gelabeld zijn met B wordt het voorwerp dichter naar de centrale as getrokken, en daarbij neemt de snelheid van het voorwerp toe.
D	Bij de delen van de omloop die gelabeld zijn met D beweegt het voorwerp zich in een richting tegen de middelpuntgerichte kracht in, en daarbij verliest het voorwerp snelheid.

(Je vraagt je misschien af of het afbuigen ook verklaard kan worden met een voorbeeld dat gebruik maakt van snelheid in een rechte lijn. Zie daarvoor de bespreking rechte lijn in de Opmerkingen sectie.)

Drukverschil toevoegen aan de weergave

De opgedane informatie kan nu worden toegepast op beweging over het oppervlak van de Aarde: de tendens om af te buigen is in alle richtingen even sterk.

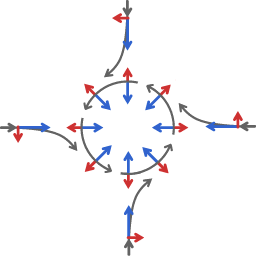
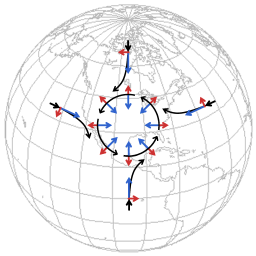
Bij de bewegingen van de atmosfeer zijn de twee belangrijkste factoren drukverschil-kracht en Coriolis effect.

De term 'drukverschil-kracht verwijst hier naar hogedrukgebieden en lagedrukgebieden. Als er verder geen andere invloed is stroomt luchtmassa van hogere druk naar lagere druk.

De volgende afbeeldingen zijn een weergave van het opbouwen van een stromingspatroon rond een lagedrukgebied.

De blauwe pijlen zijn een weergave van de tendens om van hogere druk naar lagere druk te stromen, de rode pijlen zijn een weergave van het Coriolis effect. De diagrammen zijn zeer schematisch, om te concentreren op de kenmerken die essentiëel zijn.

Bij de aanvang begint luchtmassa van alle kanten naar het lagedrukgebied te stromen. Al die stromen, vanaf het noorden, het zuiden, het oosten of het westen, etc, raken ten opzichte van hun aanvankelijke richting naar rechts afgebogen. Alles bij elkaar is het resultaat daarvan dat de verschillende stromingen elkaar bijduwen tot een stromingspatroon rondom het lagedrukgebied. Het eindresultaat is een stroming die niet van hoog naar laag gaat, maar die overal haaks staat op de richting van aflopende luchtdruk. Dat wil zeggen, in plaats van het luchtdruk verschil te vereffenen gaat de lucht er omheen stromen. Dat is de reden dat lagedrukgebieden (en hogedrukgebieden) weken in stand kunnen blijven, in plaats van dagen.

Touwtrekken

De stroming rondom het lagedrukgebied wordt gekenmerkt door een soort van touwtrekken tussen luchtdrukverschil-kracht en Coriolis effect.

Het Coriolis effect blijft op nog een andere manier actief: als het stromingsgebied in zijn geheel samentrekt dan is er een bewegingscomponent die naar binnen gericht is. Die naar binnen gerichte component wordt door het Coriolis effect weer afgebogen naar stroming haaks op de luchtdrukgradiënt. Dus niet alleen het ontstaan van stroming rondom een lagedrukgebied wordt door het Coriolis effect in de hand gewerkt, maar ook instandhouding van die stroming.

Opmerkingen

Uitdijing aan de evenaar

Het aardoppervlak is bij de evenaar ongeveer 20 kilometer verder bij het geometrisch middelpunt van de aarde vandaan dan bij de polen. Op een totale straal van de Aarde van 6400 kilometer lijkt dat een wel zeer klein verschil, en het kan verleidelijk zijn te denken dat het verwaarloosbaar is.

In het diagram is de hoek tussen de rode en de blauwe pijl overdreven om het punt te benadrukken. Bij de Aarde is de feitelijke hoek, op 45 graden breedte, ongeveer een tiende van een graad. Dat aflopende vlak van 0.1 graad levert de vereiste middelpuntgerichte kracht.

Hoeveel middelpuntgerichte kracht is er nodig om in een dag rondom de aardas te draaien? Voor 45 graden breedte levert een berekening dat er voor een voorwerp met een massa van 1 kilogram een kracht van 1.7 gramkracht nodig is. De verhouding is 1:580. Dus wat voor maateenheid je ook gebruikt voor gewicht, deel dat door 580 en je hebt de benodigde middelpuntgerichte kracht.
(Voor het geval je dat getal wil narekenen: de benodigde middelpuntgerichte kracht die ik gaf is de component parallel aan het plaatselijke oppervlak, zoals weergegeven in het diagram.)

Ik weeg ongeveer 80 kilo, en voor mij is de benodigde kracht ongeveer 140 gramkracht. Als je iets van en weegschaal bij de hand hebt, voel dan eens hoeveel 140 gramkracht is.

Verklaring met beweging in een rechte lijn?

Hier bespreek ik of het afbuigen dat zo typerend is voor het draaing-van-de-Aarde-effect ook kan worden verklaard met een voorbeeld dat gebaseerd is op beweging in een rechte lijn. Ik zal daarvoor twee gevallen bespreken, een met beweging over een parabolische schotel, en een met beweging over een plat oppervlak. Ik zal het volgende gebruiken als beslissend criterium: het draaing-van-de-Aarde-effect dat bij de atmosfeer in het spel is, is in alle richtingen hetzelfde.

Parabolische ijsbaan

Denk je in dat je je op een parabolische ijsbaan bevindt. (Dan heb je een grote bewegende constructie nodig. In Frankrijk staat een faciliteit die ervoor gebruikt zou kunnen worden. Het gaat om een ronddraaiende kuip met een diameter van 13 meter. De faciliteit wordt gebruikt om oceanografische en meteorologische modellen te toetsen. Als je de watermassa in die kuip kan bevriezen dan levert dat een parabolische ijsbaan op.)
Denk je in dat je je op die ijsbaan bevindt, de ijsbaan draait rond met dezelfde snelheid als toen hij werd gemaakt. Je geeft een tik tegen een ijshockeypuck in voorwaartse richting. Dat wil zeggen, je geeft een zodanige snelheid dat de puck sneller gaat dan de ijsbaan zelf. De puck zal dan van de centrale as vandaan bewegen.
Leg de puck weer stil, en geef een duw in achterwaartse richting: nu gaat de puck langzamer dan de ijsbaan zelf, en de puck zal naar beneden zakken, naar de centrale as toe.

Platte schijf

Nu hetzelfde experiment op het oppervlak van een ronddraaiende platte schijf. Onderstaande animatie illustreert die opstelling. Je ziet verscheidene pucks die gelijktijdig een snelheid krijgen, langs dezelfde rechte lijn, maar ieder een verschillende snelheid.

De pucks die voorwaarts bewegen gaan bij de centrale as vandaan. OK, dat is vergelijkbaar met wat er gebeurd in het geval van de parabolische schotel.

Hoe zit het met de pucks die achterwaarts bewegen? De achterwaarts bewegende pucks gaan ook bij centrals as vandaan! Ze gaan er vandaan omdat ze bewegen langs een rechte lijn die raakt aan het cirkelvormige platform. Dus bij een platte schijf gaan zowel voorwaarts als achterwaarts bewegende pucks bij de centrale as vandaan.

Het antwoord op de vraag is Nee: in Meteorologie kan de afbuiging van beweging ten opzichte van het ronddraiende systeem niet verklaard worden met een voorbeeld dat gebaseerd is op beweging in een rechte lijn.

Andere materialen op deze site

Verdere bespreking van het planetaire Coriolis effect is in het artikel Oceanografie: Inertiaaloscillaties

Tekst, afbeeldingen en animaties zijn beschikbaar gesteld voor anderen onder de volgende voorwaarden:
Creative Commons Attribution-ShareAlike 3.0 Unported License.

Laatste keer dat deze pagina is bewerkt: 18 juni 2017.