De slinger van Foucault

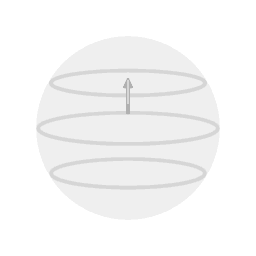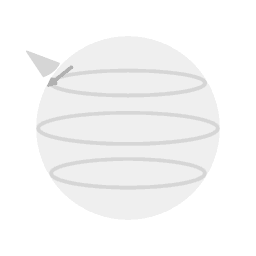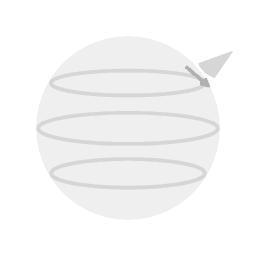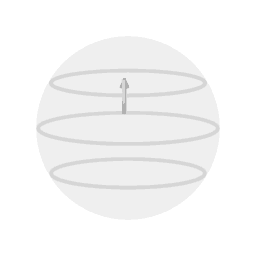
Beeld 1. Animatie
Een Foucaultslinger die zich bevindt op 30 graden noorderbreedte doet er twee dagen over om een volledige precessiecyclus te doorlopen.

Stereografische animatie
(Deze link opent een nieuwe pagina.)

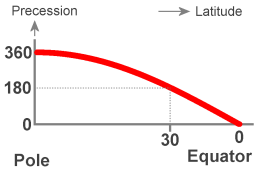
Beeld 2. Image
De precessie ten opzichte van het aardoppervlak in graden per siderische dag

Veel besprekingen van de slinger van Foucault behandelen exclusief het geval van een Foucaultslinger die zich op de noordpool of zuidpool bevindt.

(Overigens, in de permanente basis op de geografische zuidpool is door een drietal daadwerkelijk een Foucaultslinger gerealiseerd zie: South Pole Foucault pendulum Wegens grote foutmarge wetenschappelijk niet zo interessant, maar wel heel geestig.)

Dit artikel bespreekt de fysica van een Foucaultslinger die zich juist niet op de noord/zuidpool bevindt.

Een Foucaultslinger die zich bevindt op de breedtegraad van Parijs (48 graden noorderbreedte) doet er 32 uur over om een volledige precessiecyclus te doorlopen. Dit betekent dat na 24 uur, wanneer de Aarde weer in de richting staat waar ze 24 uur tevoren stond, de slinger driekwart van een precessiecyclus heeft doorlopen. Als de slinger is begonnen in noord-zuid richting, dan slingert ze na 24 uur in oost-west richting.
Animatie 1 toont een schematische weergave van het geval van een Foucault slinger die zich op 30 graden noorderbreedte bevindt. De precessie ten opzichte van het stukje aarde waar de slinger boven hangt heeft dan een periode van twee dagen; na 24 uur is het vlak van slingering 180 graden gedraaid ten opzichte van de aanvankelijke richting.

De opgave die in dit artikel wordt aangepakt is om het preciese bewegingspatroon van de slinger van Foucault te verklaren in termen van fundamentele principes. Veel besprekingen van de Foucaultslinger gaan niet in op de verklaring. Bijvoorbeeld, Hart, Miller en Mills schrijven "de hoeksnelheid van het vlak van slingering is simpelweg de projectie van de hoeksnelheid van de Aarde op de lijn die het centrum van de Aarde en het ophangpunt van de slinger verbindt." ¹ Die omschrijving is niet een verklaring van het onderliggende mechanisme, of een poging daartoe, maar enkel een beschrijving van de observatie zelf.

Dit artikel beschrijft het mechanisme dat de verandering van richting veroorzaakt in het geval van een Foucaultslinger die zich niet op de noord/zuidpool bevindt.

Gekoppelde oscillaties

Het bewegingspatroon van de Foucaultslinger omvat twee oscillaties, op verschillende grootteschalen. Op kleine schaal is er het zwaaien van de slinger, dit zal ik verder 'de vibratie' noemen. Op grote schaal is er de rotatie van de Aarde om zijn eigen as, waardoor de Foucaultslinger een cirkelbeweging rondom de aardas maakt. Een uniforme cirkelbeweging kan worden opgevat als een lineaire combinatie van twee harmonische oscillaties. Bij een Foucaultslinger is er een koppeling tussen de rotatie en de vibratie in die zin dat het meebewegen in de algemene rotatie de vibratie beinvloed. Vanwege het grote verschil in periode tussen de vibratie en de rotatie is de koppeling niet sterk. Ze lijkt verwaarloosbaar te zijn, maar de koppeling is wel degelijk significant omdat het effect cumulatief is.
Het is verleidelijk om te denken dat de centripetale versnelling de richting van het vlak van slingering niet zal beinvloeden omdat een uniforme lineaire versnelling de richting van een slingervlak niet zal beinvloeden. Echter, de richting van de centripetale kracht verandert tijdends de zwaai van de slinger, en hoewel die verandering zeer gering is van zwaai tot zwaai is het effect cumulatief en daardoor uiteindelijk significant.

Zie het artikel over Rotatie-vibratie koppeling voor een bespreking van het eenvoudigste geval van dit soort koppeling.

Table of contents

· Het Wheatstone-Foucault apparaat
· De Wheatstone slinger
· Fysische principes
    · Beweging naar de centrale as toe en er vandaan
    · Beweging tangentiaal aan de rotatie
    · De afhankelijkheid van de sinus van de breedtegraad
· Wiskundige afleidingen
    · De bewegingsvergelijking voor het draaiende coördinatensysteem
        · De twee krachten in de bewegingsvergelijking
· Overzicht: de arbeid die wordt verricht door de centripetale kracht
· Historische opmerking

Het Wheatstone-Foucault apparaat

Beeld 3. Image
Wheatstones ontwerp dat hetzelfde effect laat zien als de slinger van Foucault.

In 1851 werd een notitie van Charles Wheatstone gepresenteerd aan de Royal Society waarin Wheatstone het apparaat dat is afgebeeld in afbeelding 3 beschreef. Een transcriptie van de notitie van Wheatstone is beschikbaar bij Wikisource: Note relating to M. Foucault's new mechanical proof of the Rotation of the Earth"

De spiraalveer kan trillen als een snaar. Het cirkelvormige platform is draaibaar rond een verticale as. Deze verticale as zal ik verder 'de centrale as' noemen. Het volgende is een quote uit de notitie van Wheatstone:

"Wanneer het bovenste uiteinde van de spiraalveer op 90° wordt geplaatst, oftewel dat de spiraalveer samenvalt met de centrale as, en de spiraalveer wordt in een trilling met een bepaalde richting gebracht, laten we zeggen van N. naar Z., dan zal het in die richting blijven trillen, wat voor draaing er verder ook mag worden opgelegd aan het wiel; zodat het vlak van vibratie ten opzichte van het wiel, of ten opzichte van de as van de spiraalveer, zal bewegen met dezelfde snelheid, en in omgekeerde richting als het wiel. Wanneer de schuifclip op 30° wordt gefixeerd, en de spiraalveer dus een hoek maakt van 60° met de draaingsas zodat zijn beweging het oppervlak van een kegel beschrijft die deze hoek met de verticaal heeft, zal men zien dat het vlak van vibratie een volledige draaing maakt in de loop van twee draaingen van het wiel; dit kan het beste worden gezien door te kijken langs een verticaal vlak dat samenvalt met het verticale vlak waar de spiraalveer in ligt, waarbij men met het wiel meeloopt bij het draaien ervan. Wanneer de schuifclip is gefixeerd in een hoek van 19½º, zal het één draaing doorlopen in de loop van drie draaingen van het wiel; indien gefixeerd in een hoek van 14½º, zal het één draaing doorlopen in de loop van vier draaingen van het wiel; . &c.; en als het op 0º, waarbij de spiraalveer horizontaal ligt, dan is er geen rotatie van het vlak van vibratie. Het is niet nodig op te merken dat de sinussen van 90º, 30º, 19½º, 14½º, 0º corresponderen met de getallen 1, 1/2, 1/3, 1/4, 0, de reciproken van de getallen die de respectievelijke rotatietijden weergeven."

De slinger van Wheatstone

Beeld 4. Afbeelding
Versie van het apparaat van Wheatstone die de overeenkomst met de slinger van Foucault onderstreept.

Beeld 5. Afbeelding
Een Wheatstone-slinger opstelling met de ophangpunten palellel aan de centrale rotatie-as.

Ik zal de fysica van de Foucaultslinger bespreken door paralellen te trekken met het apparaat van Wheatstone. De kenmerken die de Slinger van Foucault en het apparaat van Wheatstone gemeenschappelijk hebben zijn de kenmerken die van belang zijn voor het begrijpen van de fysica die plaatsvindt. Om de overeenkomst met de slinger van Foucault te onderstrepen zal ik een iets aangepaste versie van het Wheatstone-Foucault apparaat nemen. Het apparaat dat is afgebeeld in afbeelding 4 noem ik 'de slinger van Wheatstone'. Het kleine balletje correspondeert met de bal van de Slinger van Foucault. De kracht die door de binnenste veer wordt uitgeoefend correspondert met de zwaartekracht die op de slingerbal werkt, en de kracht die door de buitenste veer wordt uitgeoefend correspondeet met de kracht die de ophangdraad uitoefend op de slingerbal.

In het vervolg van dit artikel zal ik door elkaar verwijzen naar de Foucaultslinger en de Wheatstoneslinger, omdat de fysische principes die er spelen dezelfde zijn.

Fysische principes

De aannames ten behoeve van het versimpelen van de analyse

De spiraalveren worden gerekend als massaloos.
De uitwijking van de slingerbal ten opzichte van de ruststand wordt gerekend als binnen de grenzen van de kleine hoek benadering.
Alleen de krachten die door de spiraalveren worden uitgeoefend worden in beschouwing genomen.

Beoordeling van de toepasbaarheid van de afbeeldingen en animaties

In feitelijke Foucault opstellingen is de verhouding van vibraties tot de rotatie in de orde van duizenden op één. In de voorbeelden is de verhouding van vibraties tot rotatie in de orde van tien tot twintig op één. In beide bereiken zijn de fysische principes hetzelfde; de overwegingen die worden gepresenteerd zijn geldig voor alle vibratie-rotatie-verhoudingen. (Echter, onder een verhouding van ongeveer 10 op 1 en naderend naar 1 op 1 valt er minder en minder betekenisvol onderscheid te maken tussen het tempo van rotatie en het tempo van vibratie.)
De precessie van het vlak van slingering is onafhankelijk van de amplitude van de slingering. Wat de amplitude van de vibratie ook is, dezelfde overwegingen zijn geldig.

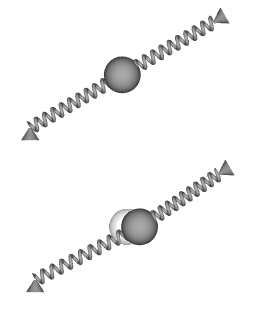
Beeld 6. Afbeelding
Bovenaan: stand in rust.
Onderaan: Verplaatsing naar buiten als het platform aan het draaien is.

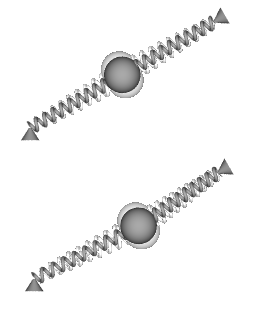
Beeld 7. Afbeelding
Bovenaan: vibratiepatroon als het platform niet aan het draaien is.
Onderaan: vibratiepatroon bij draaiend platform.

Afbeeldingen 6 en 7 tonen een detail van de slinger van Wheatstone, in verschillende toestanden van beweging.

Afbeelding 6:
Bovenaan wordt de toestand van de spiraalveren getoond als de slinger van Wheatstone niet in beweging is. Beide spiraalveren zijn even ver uitgerekt, en ze staan in elkaars verlengde. Onderaan de afbeelding wordt de verplaatsing getoond die er is als het platform draait. Als het platform draait is de binnenste veer meer uitgerekt dan in de ruststand, en de buitenste veer is minder uitgerekt dan in de ruststand, en het effect is dat de spiraalveren de benodigde centripetale kracht leveren voor de cirkelbeweging van de slingerbal rondom de centrale as.

Afbeelding 7:
De bovenkant van de afbeelding toont de vorm van de spiraalveren wanneer de slinger van Wheatstone aan het vibreren is, maar niet aan het draaien. Beide spiraalveren worden even ver uitgerekt, en op het middenpunt staan ze in elkaars verlengde. De onderkant van de afbeelding toont dat wanneer de slingerbal vibreert terwijl het platform aan het draaien is het middenpunt van de vibratie het naar buiten verplaatste punt van de slingerbal is.

Opmerking: in deze afbeeldingen is de amplitude van de vibratie iets kleiner dan de buitenwaartse verplaatsing van de slingerbal; in de gebruikelijke opstelling is de amplitude van de vibratie groter dan de verplaatsing. Interessant is hier dat dit verschil niet van belang is. Eén van de eigenschappen van de slinger van Foucault is dat de precessie van het slingervlak onafhankelijk is van de amplitude van de slingering; als de amplitude van een Foucaultslinger afzwakt blijft de precessie hetzelfde. Daarom is de weergave met de buitenwaartste verplaatsing ongeveer even groot als de amplitude van de slingerbeweging net zo geldig; de fysische principes die er spelen zijn hetzelfde als in een opstelling waarbij de buitenwaartse verplaatsing aanzienlijk kleiner is dan de amplitude van de slingering.

Beweging naar de centrale as toe en er vandaan

Beeld 8. Animatie
Schematische weervave van de beweging van de slingerbal gezien vanuit meedraaiend perspectief.

Beeld 9. Animatie
Beweging van de slingerbal van de Wheatstoneslinger gezien vanaf pal boven het platform. De hoek van de spiraalveren correspondeert met 30 graden noorderbreedte.

Laat het platform tegen de klok in draaien. Op ieder tijdstip heeft de slingerbal een bepaald impulsmoment ten opzichte van de centrale draaiingsas. Wanneer de slingerbob dichter naar de centrale as wordt getrokken verricht de centripetale kracht arbeid, en als gevolg daarvan neemt de hoeksnelheid van de slingerbal toe. (Vergelijk een kunstschaatster die om haar as draait en die haar armen dichter naar zich toe trekt om nog sneller te spinnen.) Wanneer de slingerbob van de centrale as vandaan beweegt verricht de centripetale kracht negatieve arbeid, en de hoeksnelheid van de slingerbal neemt af.

Beweging tangentiaal aan de rotatie

De hoeveelheid centripetale kracht die wordt uitgeoefend op de slingerbal is "afgestemd" op de staat van meedraaien met het systeem als geheel. De snelheid die correspondeert met meedraaien met het systeem als geheel zal 'evenwichtssnelheid' worden genoemd. Gedurende de zwaai van de slingerbal van west-naar-oost is de slingerbol de slingerbal bezig sneller om de centrale as te draaien dan de evenwichtssnelheid, en daarom zal tijdens een zwaai van west-naar-oost de slingerbal als het ware "uit de bocht vliegen". Gedurende een zwaai van de slingerbal van oost-naar-west is de slingerbal de centrale as aan het ronden met een snelheid die lager is dan de evenwichtssnelheid, en daarom zal gedurende oost-naar-west beweging de centripetale kracht de slingerbob dichter naar de centrale as trekken.

Beeld 10. Afbeelding
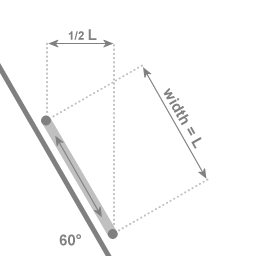
Het geval van een hoek van 60 graden met de centrale as van draaiing. Als de twee uiterste punten van de zwaai een afstand van L van elkaar vandaan liggen, dan is de beweging naar de centrale as toe en er vandaan over een afstand van 1/2 L

De afhankelijkheid van de sinus van de breedtegraad

Voor de Wheatstoneslinger geldt net als voor de Foucaultslinger dat de hoeveelheid precessie ten opzichte van het draaiende systeem afhankelijk is van hoeveel de slingerbal naar de centrale as toe beweegt en er vandaan, ten opzichte van de volledige amplitude.

In het geval van een slinger die is opgesteld op 30 graden breedte: wanneer de zwaai van het ene uiterste punt naar het andere uiterste punt een afstand L overbrugd, dan is de beweging naar de centrale as toe (of er vandaan) over een afstand van 1/2 L. Dit is bepalend voor de mate waarin de centripetale kracht het vlak van slingering zal beinvloeden. Hoe dichter bij de evenaar, hoe zwakker de koppeling tussen de rotatie en de vibratie.

Wiskundige afleidingen

De bewegingsvergelijking voor het draaiende coördinatensysteem

Wanneer de bewegingsvergelijking wordt opgesteld voor beweging ten opzichte van een draaiend coördinatensysteem is de Coriolisterm facultatief; ze is alleen nodig als het object dat wordt beschreven een snelheid heeft ten opzichte van het roterende systeem. De centrifugale term moet altijd worden toegevoegd, want ze is evenredig met de afstand tot de centrale rotatie-as.

Als er geen enkele kracht werkt geeft de volgende set vergelijkingen de bewegingsvergelijking voor beweging ten opzichte van een draaiend coördinatensysteem. In de vorm zoals hier gepresenteerd zijn de x en de y coördinaat positie ten opzichte van de centrale rotatie-as; de centrale as is het nulpunt van het gebruikte coördinatensysteem. Ω is de hoeksnelheid va het draaiende systeem.

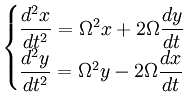
$\begin{cases} \dfrac{d^2x}{dt^2} = \Omega^2 x + 2 \Omega \dfrac{dy}{dt} \\ \dfrac{d^2y}{dt^2} = \Omega^2 y - 2 \Omega \dfrac{dx}{dt} \end{cases}$

De twee krachten in de bewegingvergelijking voor de slinger van Foucault.

De twee krachten die in de beweingsvergelijking moeten worden opgenomen zijn de centripetale kracht die de rotatie in stand onderhoudt, en de terugdrijvende kracht die de vibratie ondehoudt. Uiteraard is het zo dat zowel de centripetale kracht als de terugdrijvende kracht door de spiraalveren wordt geleverd in een enkelvoudige actie; in die zin is het puur een wiskundige truuk om te doen alsof er twee verschillende mechanismes aan het werk zijn. De wiskundige truuk is hier dat een kracht altijd kan worden ontbonden in componenten zolang de resulterende kracht van die componenten maar overeenkomt met de daadwerkelijke kracht.

De centripetale kracht die benodigd is voor het ronddraaien met constante hoeksnelheid Ω wordt beschreven met de volgende termen:

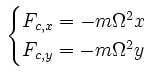
$\begin{cases} F_{c,x} = - m \Omega^2 x \\ F_{c,y} = - m \Omega^2 y \end{cases}$

De terugdrijvende kracht duwt de slingerbal terug naar het middenpunt (de richting van een loodlijn onder het ophangpunt) van de slinger. Het coördinatensysteem kan zo gekozen worden dat de de centrale as en het middenpunt allebei op de y-as liggen. Laat de y-coördinaat van het middenpunt y_e genoemd worden. Laat de frequentie van de slingering ψ genoemd worden.

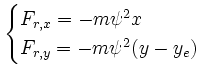
$\begin{cases} F_{r,x} = - m \psi^2 x \\ F_{r,y} = - m \psi^2 (y - y_e) \end{cases}$

De volledige bewegingsvergelijking voor de slingerbal (voor beweging ten opzichte van roterende coördinaten) bevat vier termen: de centrifugale term, de coriolis term, een uitdrukking voor de centripetale kracht, en een uitdrukking voor de terugdrijvende kracht. Die vier termen zijn vectoren, en de vector sommatie vandie termen geeft de versnelling van de slingerbal ten opzichte van het draaiende systeem.

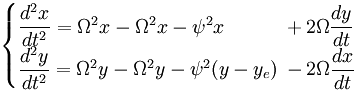
$\begin{cases} \dfrac{d^2x}{dt^2} = \Omega^2 x - \Omega^2 x - \psi^2 x & \!\!\! + \, 2 \Omega \dfrac{dy}{dt}\\ \dfrac{d^2y}{dt^2} = \Omega^2 y - \Omega^2 y - \psi^2 (y - y_e) & \!\!\! - \, 2 \Omega \dfrac{dx}{dt} \end{cases}$

Het is direct duidelijk waarom het zo praktisch is om een mee-draaiend coördinatensysteem gebruiken voor de berekeningen: de uitdrukking voor de centripetale kracht en de uitdrukking voor de centrifugale term vallen weg tegen elkaar.

Het feit dat de centrifugale term en de uitdrukking voor de centripetale kracht tegen elkaar wegvallen is geen toeval; het is een eigenschap van het fysische systeem dat hier onder beschouwing is.
Op iedere afstnd tot de centrale rotatie-as leveren de spiraalveren de houveelheid centripetale kracht die nodig is voor een cirkelvormige beweging met hoeksnelheid Ω. Het systeem is zelf-aanpassend. Bijvoorbeeld, wanneer de hoeksnelheid van het systeem toeneemt dan vervormen de spiraalveren een beetje verder totdat het punt is bereikt waar de spiraalveren de benodigde hoeveelheid centripetale kracht uitoefenen.

Volgende stap: de centrifugale term en de uitdrukking voor de centripetale kracht tegen elkaar weg laten vallen.

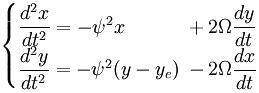
$\begin{cases} \dfrac{d^2x}{dt^2} = - \psi^2 x & \!\!\! + \, 2 \Omega \dfrac{dy}{dt} \\ \dfrac{d^2y}{dt^2} = - \psi^2 (y - y_e) & \!\!\! - \, 2 \Omega \dfrac{dx}{dt} \end{cases}$

Dit kan verder worden versimpeld door het nulpunt van het coördinatensysteem te verschuiven. De coriolis term bevat enkel de snelheid ten opzichte van het draaiende systeem, dus ze is onafhankelijk van waar het nulpunt van het coördinatensysteem wordt neergelegd. In de volgende vergelijkingewn zijn x en y niet de afstand tot de centrale rotatie-as maar de afstand tot het middenpunt van de vibratie.

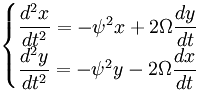
$\begin{cases} \dfrac{d^2x}{dt^2} = - \psi^2 x + 2 \Omega \dfrac{dy}{dt} \\ \dfrac{d^2y}{dt^2} = - \psi^2 y - 2 \Omega \dfrac{dx}{dt} \end{cases}$

Beeld 11. Afbeelding
Het geval van een hoek van 60 graden met de centrale as van draaiing. Als de twee uiterste punten van de zwaai een afstand van L van elkaar vandaan liggen, dan is de beweging naar de centrale as toe en er vandaan over een afstand van 1/2 L

Bovenstaande vergelijkingen zijn maar voor één specifieke situatie van toepassing, het geval dat correspondeert met een Foucaultslinger op één van de polen. Wat moet worden toegevoegd om geldig te zijn voor het algemene geval is geïllustreerd in afbeelding 11. De hoeveelheid beweging naar de centrale rotatie-as toe (of er vandaan) bepaalt de sterkte van de koppeling tussen de rotatie en de vibratie. De sterkte van de koppeling is evenredig met de sinus van de breedtegraad.

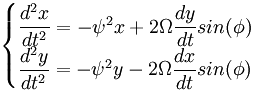
$\begin{cases} \dfrac{d^2x}{dt^2} = - \omega^2 x + 2 \Omega \dfrac{dy}{dt} sin(\phi) \\ \dfrac{d^2y}{dt^2} = - \omega^2 y - 2 \Omega \dfrac{dx}{dt} sin(\phi) \end{cases}$

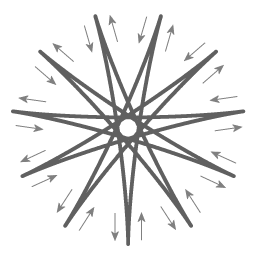
De afbeelding rechts toont een oplossing voor de bovenstaande bewegingsvergelijking met een verhouding van ψ staat tot Ω van 11 staat tot 1. (Gebruikelijk in een Foucault opstelling is een verhouding van duizenden tot één).

Het is zeer opmerkelijk dat volgens de vergelijkingen de vorm van de beweging van de Foucaultslinger hetzelfde is op alle breedtegraden, de breedtegraad bepaald enkel het tempo van de precessie. Dat is verrassend, want in het geval van een polaire Foucaultslinger en in het geval van en niet-polaire Foucaultslinger zijn de mechanismen die spelen geheel verschillend.
In het geval van een polaire Foucaultslinger is de enige fysica die er speelt het zwaaien van de slinger; het vlak van slingering blijft in dezelfde richting wijzen, en de Aarde draait daar onderdoor, zonder de slinger te beinvloeden; de "precessie" van een polaire Foucaultslinger is schijnbare precessie. Aan de andere kant, in het geval van een niet-polaire slinger is de slingeropstelling als geheel om de aardas aan het cirkelen en dat heeft een effect op de slingering: er is een koppeling van de cirkelbeweging en de slingering, met als gevold een daadwerkelijke precessie van het zwaaivlak van de slinger.

Overzicht: de arbeid die wordt verricht door de centripetale kracht.

In de bewegingsvergelijking voor beweging ten opzichte van een draaiend coördinatensysteem zorgen de centrifugale term en de coriolis term ervoor dat de coördinatentransformatie in rekening wordt genomen. De centrifugale term en de coriolis term zijn rekenkundige instrumenten die onder bepaalde omstandigheden een versnelling van de berekening mogelijk maken. (Vergelijk bijvoorbeeld het gebruiken van complexe getallen in berekeningen aan electronische componenten. In de berekeningen heeft de wisselstroom die er loopt een reële component en een imaginaire component. Deze imaginaire component bestaat niet, ze wordt alleen maar toegevoegd om het afhandelen van de berekening versnellen. Zie voor meer informatie the Scot's guide to electronics.)

De fysica die er speelt wordt verklaard door de effecten van de centripetale kracht te volgen: wanneer de slingerbal naar de centrale rotatie-as beweegt verricht de centripetale kracht arbeid, en wanneer de slingerbal van de centrale rotatie-as vandaan beweegt verricht de centripetale kracht negatieve arbeid.

Historische opmerking.

Gustave Gaspard Coriolis ondernam theoretisch onderzoek naar de efficiëntie van waterraderen. In de openingsparagraaf van het in 1731 gepubliceerde artikel noemde Coriolis dat Bernouilli het geval had geanalyserd van welke kracht er werkt op een voorwerp dat vrij kan schuiven in een horizontale buis die ronddraait. Coriolis had toen de taak op zich genoemn om ge meest algemene formules uit te werken, formules om iedere beweging te kunnen beschrijven. Met deze formules zou Coriolis voor iedere vorm van het watervoerende onderdeel kunnen berekenen hoeveel arbeid er zo kunnen worden verricht. In de loop van het afleiden van formules was één van de termen die oprees de term waar heden ten dage naar wordt verwezen als 'de Coriolis term'.

De onderzoekingen van Coriolis betroffen het verrichten van arbeid, zijn onderzoekingen betroffen energieomzetting. En in het geval van een slinger van Foucault die zich niet op één van de polen bevindt is de daadwerkelijke precessie een gevolg van arbeid die wordt verricht door de centripetale kracht. Dat houdt dus in dat het mechanisme dat de daadwerkelijke precessie van de slinger van Foucault verklaard het onderwerp was van de onderzoekingen van Coriolis destijds.

De belangrijkste bronnen van informatie voor dit artikel:

Persson, A., 1998 How do we Understand the Coriolis Force? Bulletin of the American Meteorological Society 79, 1373-1385.

Phillips, N. A., What Makes the Foucault Pendulum Move among the Stars? Science and Education, Volume 13, Number 7, November 2004, pp. 653-661(9)

Noten:

noot 1
John B. Hart, Raymond Miller, Robert L. Mills, A simple geometric mode for visualizing the motion of a Foucault pendulum American Journal of physics 55(1), January 1987

Tekst, afbeeldingen en animaties zijn beschikbaar gesteld voor anderen onder de volgende voorwaarden:
Creative Commons Attribution-ShareAlike 3.0 Unported License.

Laatste keer dat deze pagina is bewerkt: 18 juni 2017.

·	Rotatie-vibratie koppeling
·	Inertiaaloscillaties
·	Vergelijking van inertiaaloscillaties met ballistische beweging
·	De slinger van Foucault
·	Het Eötvös effect
·	Coriolis debietmeter