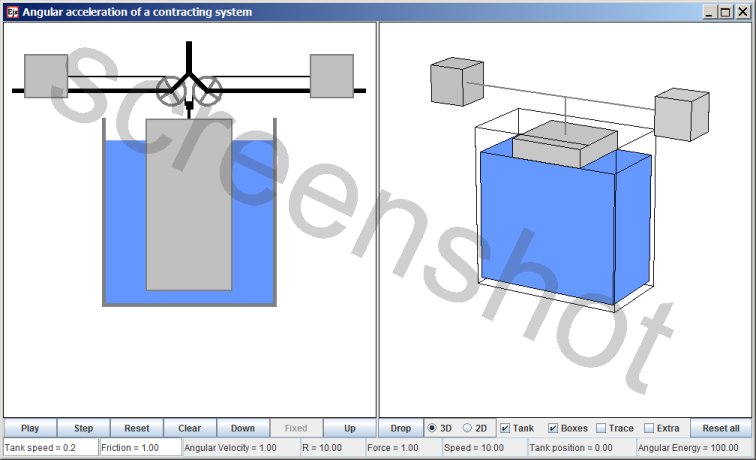
This image is smaller than the actual simulation. Clicking on it starts a download of the standalone Angular acceleration simulation (requires Java)

Angular acceleration of a contracting system

To sustain rotating motion a centripetal force is required. If there is a surplus of force the rotating system will contract. The simulation illustrates that when the centripetal force has contracted a rotating system to half its initial radius then:
- The tangential velocity has doubled
- The angular velocity is 4 times faster
- The rotational kinetic energy is 4 times higher
- The required centripetal force is 8 times stronger

The blue area represents a fluid, and the tank that holds the fluid can be raised or lowered. A large mass is immersed in the tank. Cables run over pulleys to a pair of weights that is circumnavigating a central axis of rotation. The weight of the central mass provides centripetal force.

When the central mass is lifted out of the fluid the centripetal force increases. For simplicity the density of the fluid is equal to the density of the mass, so that the centripetal force is exactly proportional the part of the central mass that is not immersed; the buoyancy design allows you to see at a glance how much centripetal force is being exerted.

The default setup is one in which the playing simulation will throughout remain close to an equilibrium state. The button 'Drop' sets up beginning conditions that are the opposite: as far out of equilibrium as possible.

Adjustable variables

There are two editable fields:

Tank speed Determines how fast the tank drops or ascends.
(Entering too large a value can be fun, but it will give unphysical results.)
Friction A friction factor that acts purely in radial direction.
For instance, when the central mass descends into the fluid it will cause turbulence. Causing the turbulence acts as friction; some of the energy is dissipated.

Evolution of the simulation

Each of the circumnavigating masses has a mass of one unit of mass. At the start the angular velocity is 1 radian per second. The initial radial distance to the central axis is set at 10 units of length, because 'g', the gravitational acceleration, is 10. The exact values of the variables are not important, what is important is their ratios before and after the contraction.

There are three buttons that control the position of the tank: 'Down', 'Fixed', and 'Up'. Pressing the 'Down' or 'Up' button sets the tank in motion, pressing the 'Fixed' button halts the motion of the tank. The simulation is safe-guarded against dropping the tank too low; when the tank threatens to descend so low that the central mass ends up hanging above the fluid level the tank motion is suspended, only to resume when tank motion is possible without triggering the safe-guard. Likewise, there is a safe-guard against immersing the central mass too deep.

The centripetal force

The buoyancy design ensures that throughout the simulation the centripetal force is close to what is required to sustain circumnavigation with a constant radius. When there is a surplus of force the rotating system contracts, accelerating in the process. The system accelerates because the centripetal force is doing work.

It may sound strange that the centripetal force is doing work. Both at the start and at the end the velocity is perpendicular to the direction of the centripetal force as the motion is circular then, and we have been taught that in the case of circular motion the centripetal force is not doing work. However, during the contraction the trajectory is a spiral, and then the instantaneous velocity is not perpendicular to the force. That gives the centripetal force the opportunity to increase the speed.

Plunge

The button 'Drop' sets up a demo that is mainly intended for fun. The starting situation is as far away from any equilibrium as possible, and the friction is set to a very low value, too low to be physically realistic.

However, one aspect of that 'violent plunge' demo is a true reflection of physics. Eventually the motion in radial direction subsides, and the simulation settles in a pattern of circular motion. There is friction only for motion in radial direction, so when the motion has become circular there is no more opportunity for dissipating energy. A lot of kinetic energy and potential energy remains, but that can no longer dissipate.

Implication of the centripetal force doing work

The simulation is set up in such a way that there is no friction to rotating motion. That means that all the work that the centripetal force is doing is converted to energy of rotating motion.

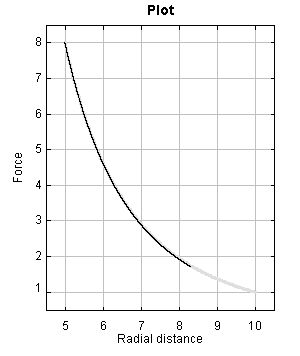
Picture 1. Diagram<br> Two objects, R and T, moving with constant momentum. Hence the momentum of the common center of mass, S, is constant.

Picture 1. Diagram
The thick lightgrey line represents the analytic function y=1/x³

The checkbox 'Extra' opens a second panel in which the centripetal force is plotted against radial distance. In the diagram a line is already present, that line represents the following analytic function:

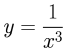
$y = \dfrac{1}{x^3}$

As you can see, the plot of the centripetal force against the radial distance follows exactly that shape (the slower the tank descends and ascends the closer the match). So we have in this case:

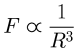
$F \varpropto \dfrac{1}{R^3}$

The symbol ∝ means: 'is proportional to'. In the following formulas the angular velocity is denoted with ω, the greek letter 'omega', and the radial distance is denoted with 'R'. For a given ω and R the required force is proportional to ω²R

$F \varpropto \omega^2R$

Combining the previous two expressions:

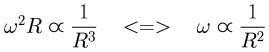
$\omega^2R \varpropto \dfrac{1}{R^3} \quad <=> \quad \omega \varpropto \dfrac{1}{R^2}$

Which rearranges to:

$\omega R^2 = C$

Where C is a constant. What is this conserved quantity ωR² ? If you multiply it with the mass then you get mωR², which is angular momentum.
The simulation illuminates the underlying physics of conservation of angular momentum. When the centripetal force has contracted a rotating system to half its previous radius it has increased the angular velocity fourfold.

The change in kinetic energy equals the work that is being done. ΔE = F *Δr. In this case the instantaneous centripetal force is a function of the amount of work that has been done up to that point, so the relation must be recast in differential form

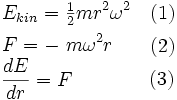
Substituting the expressions for E and F into the differential equation (3) gives:

In the equation below ω has been substituted with C/R², and the reader can verify that the equation is satisfied.

Method of computation

The method of computation is numerical analysis: the trajectory of the particle is calculated by evaluating differential equations.

This simulation has been created with EJS
EJS stores the specifications of a simulation in a plain text file, with extension .xml
You can examine how the simulation has been set up by opening the simulation .xml file with EJS.
Download location for the EJS software
Download location for the Angular acceleration source file
(The file is zipped because a browser will attempt to parse any .xml file.)

This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.

Last time this page was modified: June 18 2017