The general theory of relativity
The following exposition of the general theory of relativity does not follow the historical chain of events, even though many historical events are discussed. I present newtonian dynamics in such a way that a transition to relativistic dynamics is prepared for as much as possible.
This article relies on the reader being comfortable with the preceding article about special relativity.
Preparation: Newtonian dynamics
Fields
In the course of the 19th century it became customary to understand the laws governing motion of particles in terms of fields. Physicists began to think about electrically charged particle as the origin of a field, and other particles may interact with that field. Rather than assuming that particles exert a force directly on each other the existence of a field is assumed, with the field acting as mediator of the interaction. The field cannot be observed directly; only the consequences are observable. The observations can also be accounted for in terms of a theory in which particles exert a force directly on each other, but over time scientists noticed that a theory in terms of an interaction mediating field is more economic. The field concept facilitates an economy of thought, and in the history of physics favoring the theory that offers the best economy of thought has proven to be a good strategy many times.
Naturally the question arose whether it would be possible to frame a field theory of gravitation. Is gravitational interaction mediated by a field?
Inertia and the concept of coupling to a field
Before turning to gravitation, I will discuss inertia.
Inertia is opposition to change of velocity. For instance, if you take a slingshot and you shoot a marble at a chunk of clay the marble will penetrate into the clay because of its inertia. It's interesting to contemplate what this says about inertia. Think of pushing a stick into the clay. It takes a serious force to press the stick into the clay, and in order to exert that kind of force you have to brace yourself. More generally, I will refer to this as a need for leverage; without leverage it's not going to happen. So, what gave the marble the leverage to penetrate the clay? It's no good saying that the marble's momentum carried it into the clay, that's just empty words. The leverage that the marble needs cannot be innate to the marble. (Compare the Baron von Münchhausen story where he was sinking into a swamp. He pulled himself out of the bog by grabbing his own hair and pulling himself up with all the strength he had! If you think the Münchhausen story is unphysical then it will also be obvious to you that the marble cannot push itself into the clay.)
The marble's leverage to penetrate the clay must come from coupling to something that is not part of the marble itself. Given the well-proven power of the field concept in electromagnetism it's a natural move to hypothesize that the marble couples to an inertia field; a uniform all-pervasive field with the property that it opposes change of velocity of objects that couple to the field.
The electric charge of a particle is a measure of how strongly it couples to an electric field. Accordingly the inertial mass of a particle is a measure of how strongly it couples to the inertia field.
Inductance
For an overview of the properties of the inertia field, reviewing the somewhat analogous phenomenon inductance is helpful. A coil of conducting wire with self-induction has the following property: it will offer little resistance to current, but it will oppose any change of current strength. (If the coil is cooled down to a temperature at which superconductance occurs, the coil wil offer zero resistance to current.) The mechanism of opposing change of current strength is as follows: change of current strength induces a changing magnetic field, which in turn induces an electric field that opposes the change of current strength.
In a wire with zero resistance and zero self-induction, applying a voltage would result in an instantaneous jump to an infinitely strong current.
In a wire with some resistance and no self induction, applying a voltage results in a jump to a particular current strength (with the magnitude of the current strength described by Ohm's law: V=I*R)
In a wire with no resistance and some self-induction, and starting with zero current strength, applying a voltage results in a steadily increasing current strength. That is, if only self-induction is involved, the rate of change of current strength is proportional to the applied voltage.
The case of no resistance and some self-induction is the one that inertia is analogous to. The rate of change of velocity is proportional to the applied force.
While the analogy between inductance and inertia is intriguing it does not in itself explain inertia; in the case of the inertia field no mechanism is known. All that is possible is to describe the properties of the inertia field and how particles interact with it. That is what Newton's laws of motion do.
Newton's laws of motion
Newton's first and second law of motion can be understood as the axioms of a theory of the inertia field. (Of course those laws weren't formulated with an inertia field in mind, the concept of a field was not available in Newton's time, but they can readily be reinterpreted in that way: no discrepancy arises.)
Newton's first law:
In retrospect we recognize that opting to use euclidean geometry for representing inertial space is in itself a theory of physics. Quite understandably, Newton and his contemporaries did not regard using euclidean geometry to represent inertial space as a theory of physics; at the time there was no alternative for euclidean geometry, and euclidean geometry was perfectly adequate for the purpose! Newton's first law (reinterpreted from a modern perspective) asserts that euclidean geometry is an appropriate physics model for the isotropy and homogeneity of the inertia field. In the absence of a force the object will move along a euclidean straight line.
Definition of Force:
In newtonian dynamics, force is defined as follows: it is the interaction between a pair of objects, with each object's momentum being changed by the force exerted by the other object. It's crucial to note that by opting to define force in that way inertia is not included in the category "force". The concept of force could have been defined otherwise, how to define 'force' is a matter of choice, but once a definition is in place it's necessary to keep all subsequent statements consistent with it. Whatever you do, you cannot refer to inertia as a force; inertia falls in a category of its own.
Newtons second law:
The inertia field opposes change of velocity. In order to change velocity with respect to the inertia field, a force must be exerted. The rate of change of velocity is proportional to the applied force.
Note that in order to achieve change of velocity a pair of objects must be present, and that there must be an interaction between those two objects. By exerting a force upon each other they both change the other object's velocity relative to the inertia field.
Inertia field
To be sure, the above considerations do not prove the existence of an inertia field. What can be shown is that postulating an inertia field facilitates an economy of thought, and throughout the history of physics that has always been an important consideration.
The equivalence class of inertial coordinate systems
The symmetries of the inertia field define an equivalence class of coordinate systems: the class of inertial coordinate systems. The criterium for distinguishing an inertial coordinate system from a non-inertial coordinate system is that in an inertial coordinate system the laws of motion hold good. (This is discussed in more detail in the article Inertial coordinate system)
Spacetime
The electromagnetic field is assumed to be an occupant of space, or in terms of relativistic physics, an occupant of spacetime. The concept of the inertia field extends way beyond that. The inertia field is not an occupant of spacetime; Minkowski spacetime and the inertia field are regarded as one and the same entity.
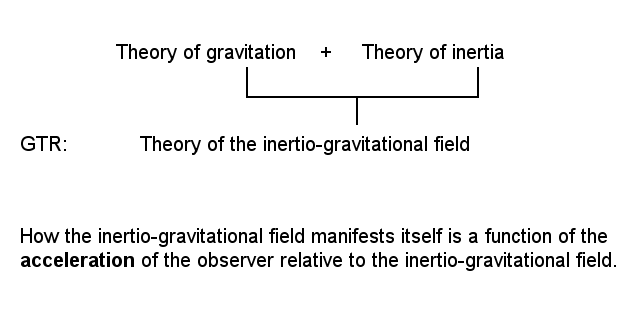
Unification: general relativity
Whereas the special theory of relativity is strictly a theory of motion, the general theory of relativity is both a theory of motion and a theory of gravitation.
In terms of the general theory of relativity both inertia and gravitation are accounted for in terms of interaction with a single field, and an appropriate name for this single field is the inertio-gravitational field. (The expression 'inertio-gravitational field' is relatively new. See documentation for a list of authors who have started using that expression.)
In terms of newtonian dynamics there is conceptually a distinction between inertial mass and gravitational mass. It is noted of course that the inertial mass and the gravitational mass always coincide, but newtonian dynamics does not account for this equivalence.
In terms of general relativity distinction between inertial mass and gravitational mass does not enter as a matter of principle: objects couple to a single field, the inertio-gravitational field. Inertial mass and gravitational mass aren't just thought of as having the same value; inertia and gravitation are thought of as arising from the same coupling.
To see how it is possible to formulate a theory of gravitation starting from the postulate of the single inertio-gravitational field it is helpful to explore acceleration in Minkowski spacetime.
Acceleration in Minkowski space-time
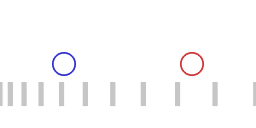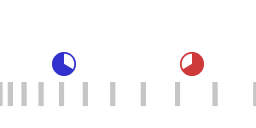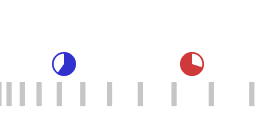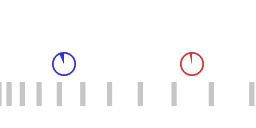
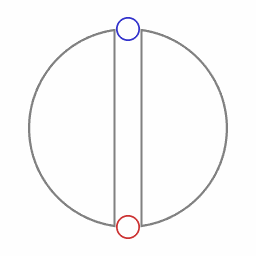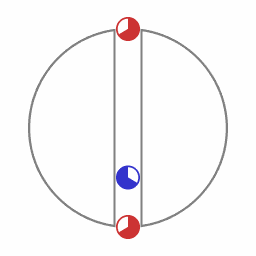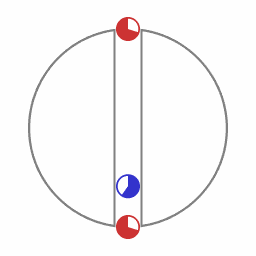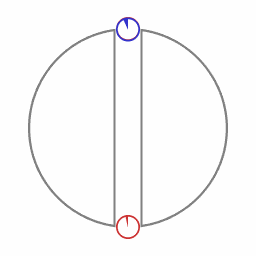
Two accelerating spaceships, the red ship chasing the blue ship.
Animation 1 represents two accelerating spaceships with the "red ship" following the "blue ship". The two ships are exchanging light signals (not shown) to maintain a constant separation. The red ship adjusts its acceleration in such a way that the transit time of a round trip of the light signal remains the same. When the roundtrip time of the light signal remains the same, the following applies:
- The red ship is accelerating harder than the blue ship, that is: the red ship is pulling more G's.
- Signals emitted by the blue ship are on reception by the reds blueshifted as measured by the reds.
- Signals emitted by the red ship are on reception by the blues redshifted as measured by the blues.
- For the blue ship a larger amount of proper time elapses than for the red ship.
Let me take a closer look at that time dilation effect. Take the case where the two spaceships are together in the beginning. First one starts to accelerate, then the other starts to follow, and for a duration of time the state of the red ship following behind the accelerating blue ship is maintained. This state is maintained far longer than the time it takes them to separate, or to rejoin later. When the two ships finally rejoin it will be seen that for the blue ship more proper time has elapsed than for the red ship. The important fact here is that the time dilation effect is not some illusion due to transmission delay: it's an actual physical effect.
Animation 1 does not represent a Minkowski spacetime diagram, for in the animation there is no global coordinate time, and no global standard of length. The vertical bars that move from left to right in the animation represent how the motion of inertially moving objects would be perceived by the red and the blue ship.
Circular motion in Minkowski space-time.
Animation 2 shows two spaceships in circular motion. In this animation the diameter of the circle of circular motion is rather small. Now consider circular motion along a circle with an extremely large diameter. The situation is then very close to being indistinguishable from the situation depicted in animation 1, which depicts linear acceleration. This indistinguishability can be seen as a form of the principle of relativity of inertial motion. In the case of motion along a circular path there is a large sideways velocity, a uniform velocity perpendicular to the direction of acceleration. But in Minkowski space-time uniform velocity is relative.
An object that is released by the blue ship will from that moment on be moving inertially. It will then accelerate with respect to the blue and red ship, accelerating (while moving inertially) towards the red ship.
Mediator of gravitational interaction
Half of the story is that the inertia field is regarded as acting upon inertial mass: when an object travels along a path in spacetime that is not the spatially shortest path then there is less lapse of proper time as compared to travelling along the spatially shortest path. In the general theory of relativity this is complemented with the assumption that the inertia field is not immutable, but that it is acted upon by inertial mass. In the general theory of relativity it is assumed that in the presence of inertial mass the inertia field is deformed away from isotropy, and this deformation of the inertia field subsequently acts as the mediator of gravitational interaction. When the quantity of mass is sufficiently large, such as the quantity of mass of a planet, the effects of the deformation of the inertia field are very noticable.
An infinitely large slab of matter generates a uniform gravitational field.
Animation 3 shows two spaceships and the grey area represents a sideways view on a slab of matter that is infinite in size. Such an infinite slab of matter would alter the physical properties of the inertio-gravitational field in a uniform way. In order to keep their distance to the slab the same, the spaceships must use thrusters. As is the case with animation 1, the animation does not represent a Minkowski spacetime diagram, for there is no global coordinate time, nor a global standard of length.
The assumption of just a single field, the inertio-gravitational field, implies that the situation depicted in animation 3 must be equivalent to the situation of animation 1 in all aspects of physics.
The uniform gravitational field that would extend away from an infinitely large slab of matter is physically unrealistic, of course. The purpose of animation 1, 2, and 3 is to focus on the concept of the inertio-gravitational field as a single field, and to illustrate the properties. A uniform gravitational field is inherently undetectable. If the two space-ships can only perform transit time measurements on signals that they are exchanging with each other (that is, only local measurements) then presence or non-presence of the infinitely large slab of matter is inherently undetectable. Given the assumption of the single inertio-gravitational field a uniform gravitational field has only a relative existence.
The gravitational field that extends away from a lump of matter such as a planet is a non-uniform gravitational field. The gravitational field that extends away from a planet is characterized by tidal effects, which are not relative.
Gravitational time dilation
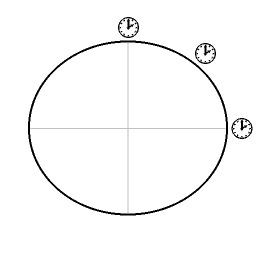
All over the world, clocks located at sealevel will count the same amount of proper time.
Picture 4 shows the Earth, with its equatorial bulge very much exaggerated. For clocks located on Earth there are two factors that determine the amount of proper time that elapses. One factor is gravitational time dilation. Clocks located near the poles are closer to the Earth's center of mass; they are located deeper in the potential well, which corresponds to a smaller amount of proper time that elapses, as compared to objects located less close to the Earth's center of gravitation. The other factor is velocity time dilation. Objects that aren't located on either of the two poles are circumnavigating the Earth's axis, which corresponds to more velocity time dilation (smaller amount of proper time elapsing) than for objects located at the poles. The closer to the equator, the more velocity time dilation.
For a clock located somewhere between the poles and the equator the total time dilation can be understood as a combination of gravitational time dilation and velocity time dilation. For all terrestrial clocks the two effects add up to the same total amount of time dilation. Thus for all terrestrial clocks located at sealevel the same amount of proper time elapses; the Earth's sealevel is an isochrone. This state of the same amount of proper time elapsing all over the Earth's surface is a state towards which the system naturally evolves. For example, suppose that the Earth rate of rotation has slowed down somewhat, but that the equatorial bulge has not decreased yet. Then instead of equilibrium a larger amount of proper time elapses at the equator than at the poles. A difference in lapse of proper time corresponds to a difference in potential energy, and this difference tends to even out; there will be a shear stress in the solid Earth. Over time there will be a redistribution of the Earth's mass toward a smaller equatorial bulge, until the amount of lapse of proper time is the same all over the Earth's surface. (Remark: the distinction between gravitational time dilation and velocity time dilation is helpful for recognizability, but as seen from a deeper level it's an artificial distinction. As seen from a more profound level the distinction isn't there - but that's beyond the scope of this article.)
In the discussion above, only gravitational time dilation is discussed. Gravitational time dilation is one aspect of curvature of spacetime. A theory of gravitation that would only incorporate gravitational time dilation would in particular yield wrong predictions for very fast motion.
General relativity describes that gravitational deflection of light that just grazes the sun will be 1.75 arcseconds. A theory of gravitation that would only incorporate gravitational time dilation would predict half that value: 0.83 arcsecond. In fact, in a 1912 paper by Einstein on an early exploratory theory of gravitation that value was stated: 0.83 arcsecond.
A theory of gravitation that would only incorporate gravitational time dilation would predict planetary orbits that are very close to orbits described by newtonian dynamics and general relativity, but it would not correctly predict the precession of the planet Mercury. The actual general theory of relativity involves deformation of spacetime; both time and space are affected.
Motion along a geodesic
According to special relativity there is a connection between inertial motion and the amount of lapse of proper time. When a set of trajectories that bring an object/observer from event A in spacetime to event B is compared, then the inertial motion trajectory is seen to have the largest amount of lapse of proper time. Why motion in spacetime has this property is not known.
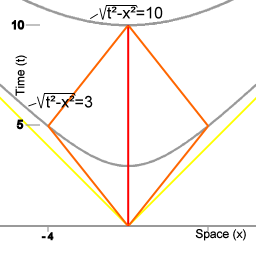
The trajectory with only inertial motion (continuous straight line in de diagram) corresponds to a maximum in lapse of proper time. For all trajectories in which more spatial distance than that is travelled, there is less lapse of proper time.
According to the general theory, the only way of describing inertial motion is in terms of that connection between inertial motion and the amount of lapse of proper time. The general theory describes that in the presence of matter physical properties of space-time are changed away from isotropy. This change of the properties of space-time away from isotropy, which is referred to as 'curvature of space-time' acts as the mediator of gravitational interaction. Given a curvature of spacetime, a trajectory that from afar is seen to be curvilinear can be the trajectory with the largest amount lapse of proper time.
The general theory replaces Newton's first law with a more general law: objects in inertial motion move along the trajectory that is the trajectory along which the amount of proper time is the largest possible.
Wheeler's antipode-antipode corridor
John Wheeler has introduced the example of a corridor drilled through a planet to illustrate the concept of moving along a geodesic. A tunnel is constructed that connects in a straight line two point of a planet that are on opposite locations on that planet. The tunnel diameter is so small compared to the size of the planet that the difference in mass distribution is negligable.
When a capsule is released at one entrance to the corridor, it will from that moment on be oscillating in that corridor. In the case of the Earth the period of one oscillation would be about 90 minutes, the same amount of time as a circular orbit that circumnavigates the Earth at very low altitude. Given the properties of the space-time that the capsule is in, the oscillating trajectory is the path that corresponds to the path with the largest possible amount of lapse of proper time. If there would also be some friction, then the capsule would eventually come to rest at the midpoint of the corridor.
A counterintuitive aspect is that one hand it is stated that objects will tend to follow the trajectory that maximizes the amount of proper time that elapses, and on the other hand it is stated that objects tend to move towards the lowest point of the gravitational well. (The lower in the gravitational well the less lapse of proper time). That raises the question: if objects tend to move along a trajectory that maximizes lapse of proper time, then why do object move towards a region where less proper time elapses? The determining factor is that for an object that moves in free fall from one altitude to another more proper time elapses than in a state of being fixed at either of the two altitudes. (Here the state of 'free fall' also applies for ascending motion. An object that is thrown upwards is also in free fall during its rise to its highest point.)
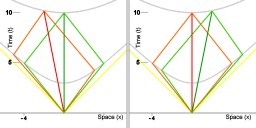
The blue object follows the path with the largest lapse of proper time.
By analogy with euclidean geometry, this path that corresponds to an extremum is called a 'geodesic'. In euclidean geometry, a geodesic is the path with the shortest possible spatial length. In the general theory of relativity, the expression 'geodesic' refers to the path with the largest amount of lapse of proper time.
An accelerometer onboard the capsule would at all times measure zero acceleration; the capsule that is oscillating in the corridor is in inertial motion. On the other hand, objects that are at rest on the surface of the Earth are not in inertial motion. For an object at rest on the surface of the Earth the local inertial frame is accelerating towards the center of the Earth. An object at rest on the surface of the Earth is (due to the normal force exerted by the Earth's surface) being accelerated with respect to the local inertial frame.
In Minkowski space-time, the equivalence class of inertial coordinate systems is globally valid. In space-time as described by general relativity, the equivalence class of inertial systems at one point in space can be accelerating with respect to the equivalence class of inertial systems at another point. In the case of the solar system one can distinguish a hierarchy. A spacecraft that is in orbit around the Moon is in inertial motion. The center of mass of the Moon in in inertial motion around the common center of mass of the Earth-Moon system. The common center of mass of the Earth-Moon system is in inertial motion around the Sun. The center of mass of the solar system is in inertial motion around the center of the galaxy.
Analogies between two fundamental unifications
Each plane of simultaneity can be seen as cutting a different cross-section of Minkowski spacetime.
Picture 7 is an illustration that was used in the article about special relativity. Every relative velocity has a corresponding distribution of coordinate time and coordinate distance. For every object/observer in spacetime there is a particular plane of simultaneity that is co-progressing in time with the object/observer. For each observer a particular slice of spacetime is valid; the slice that corresponds to his proper plane of simultaneity.
In the case of the electromagnetic field the observer's velocity relative to the electromagnetic field is the determining factor for what the observer will measure. In the four-dimensional world of Minkowski spacetime, the electromagnetic field is a single field. To any observer, there are apparently two fields: an electric field and a magnetic field. For observers at different velocities, the electromagnetic field "decomposes" differently in an electric component and a magnetic component.
In the case of the inertio-gravitational field, the determining factor for what an observer will measure is the acceleration of the observer with respect to the field. For observers that are accelerating at different accelerations with respect to the local inertio-gravitational field the field manifests itself differently.
The two unifications:

Analogies between two transitions
The following paragraphs are designed to highlight the remarkable parallels between the transition from newtonian mechanics to special relativity on one hand, and the transition from special relativity to general relativity on the other hand.
In the case of classical electrodynamics it is technically possible to formulate a theory in which it is assumed that there is an actually present background of newtonian absolute space and absolute time. Such a theory needs to find a way to accomodate the equivalence of the class of inertial coordinate systems. In such an ether theory, having a velocity with respect to the ether results in time dilation and length contraction effects that act in such a way that the assumed Newtonian background is rendered unobservable. Any theory that assumes separate space and time needs additional hypotheses to account for the fact that no experiment ever detects uniform velocity with respect to the presumed immutable Newtonian background. Special relativity has no such need because velocity with respect to spacetime does not enter special relativity.
In the case of special relativity it is technically possible to formulate a theory of motion and gravitation in which it is assumed that there is an actually present immutable Minkowski spacetime. That is: a theory that assumes a separate inertia field and gravitational field. Such a theory needs to find a way to accomodate the equivalence of gravitational and inertial mass. It turns out that a theory that assumes an immutable Minkowski spacetime needs to be amended by assuming time dilation and length contraction effects that act in such a way that the immutable Minkowski background is rendered unobservable. Any theory that assumes a separate inertia field and gravitational field would need additional hypotheses to account for the fact that no experiment ever detects uniform acceleration with respect to the assumed immutable background. General relativity has no such need because assumption of a fixed background does not enter general relativity.
Transition: replacing the metric of spacetime
In the article about special relativity I discussed that in the transition from newtonian dynamics to special relativity the spacetime metric was replaced: a shift from Euclidean metric to the Minkowski metric. In the transition from the special theory of relativity to its successor, the general theory of relativity, once again the metric was replaced. The metric that applies in the case of the general theory of relativity is called a 'Riemannian metric', as the metric allows for curvature of spacetime. This metric has a (+,-,-,-) signature; any tangent spacetime of it is described by the Minkowski metric.
Thus both the transition from newtonian dynamics to the special theory of relativity and the transition from the special theory of relativity to the general theory of relativity can be seen as replacing the preceding spacetime metric with a more generalized spacetime metric. In each case the predecessor's metric is a limiting case of the metric that replaced it. In the limit of velocity approaching zero the Minkowski metric reduces to the Euclidean metric. In the limit of spacetime curvature approaching zero the Riemannian (+,-,-,-) signature metric reduces to the Minkowski metric.
No fixed background
John Wheeler has coined the phrase: "spacetime is telling matter/energy how to move, matter/energy is telling spacetime how to curve." That is, in general relativity, the curvature of spacetime is a dynamic variable.
In Newtonian dynamics the purpose of writing down and solving the equation of motion is to find the motion of material objects with respect to the background. Solving equations of motion in Newtonian dynamics can be hard at times, but at least there is a fixed background: inertia. In general relativity, the purpose of writing down and solving the field equations is to find expressions of how the shape of the inertio-gravitational field evolves over time, and how the motion of objects evolves over time.
Let me elaborate on the above. When the purpose is to calculate a perfectly circular orbit then there is one factor that is not constant, the instantaneous direction of velocity. The other factors are constant: the distance to the center of rotation, the magnitude of the orbital velocity and the magnitude of the centripetal force. The case of a perfectly circular orbit readily yields to analysis and Huygens had derived a formula for the required centripetal force. But an orbit with some eccentricity is much harder to analyse. In the case of a keplerian orbit all the participating factors are in flux. Distance to the primary is affected by the velocity and the centripetal force, the velocity changes because of the centripetal force, the magnitude of the centripetal force is a function of the distance to the center of rotation. All of the factors are functions of each other - no starting point for a derivation. To overcome this problem Newton developed a new branch of mathematics, which he called 'fluxion reckoning'. Today this kind of mathematics is called differential calculus. The power of the differential calculus allows the calculation to be lifted over the problem of not having a starting point. The reason that the problem can be solved after all is that the participating factors can all be expressed as functions of each other.
As mentioned above, in solving the equations of newtonian dynamics space and time provide a constant background. So in fact not all of the participating factors are in flux. It is in the case of the problem posed by general relativity that really all participating factors are in flux. The inertio-gravitational field is curving as affected by distribution of matter in spacetime, with matter moving as affected by curvature of spacetime. Now there is really no starting point at all.
The equations of general relativity rely on a sophisticated mathematical apparatus that handles coordinate transformations, thus allowing equations to be expressed in a way that is not committed to a particular choice of coordinate system. The class of coordinate mappings that is supported by this apparatus is called the diffeomorphism class. Members of the diffeomorphism class can be transformed into one another by a transformation that does not "tear" or "cut" the "fabric" of space-time. That is, two points in space-time that are adjacent in one member of the diffeomorphism class are also adjacent points in all other members of the diffeomorphism class. Other than that, the mathematical apparatus accommodates a vast range of transformations: translation, uniform acceleration, any acceleration, rotation with constant rate, rotation with variable rate, any "flexing" deformation, etc.
Employing the mathematical apparatus that allows equations to be expressed in a form that is not committed to any choice of a particular coordinate system (among the diffeomorphism class) is called 'using coordinate-independent equations'. General relativity uses coordinate-independent equations to express certain physical properties. The physics of "matter/energy telling space-time how to curve, and curved spacetime telling matter/energy how to move" can be expressed in an coordinate-independent way. That is, the mathematical power of diffeomorphism invariance makes it possible to formulate equations even with the background itself being a dynamic variable. When a solution to the equations is obtained, the final step is to choose a coordinate system and map the solution to that coordinate system.
Matter, energy, fields and spacetime
In the introduction it was mentioned that the electromagnetic field can carry momentum, indicating that fields and matter are not as different as one might expect.
Electrodynamics describes that an oscillating electrically charged particle will radiate electromagnetic waves. The process of emitting electomagnetic waves decreases the kinetic energy of the oscillating particle.
General relativity describes that when two masses are orbiting each other in non-circular orbits, then that system will radiate gravitational waves. That is: gravitational waves (propagating undulations of the inertio-gravitational field) can carry away energy and momentum from a system of orbiting masses. General relativity indicates that Matter, Energy, Fields and Spacetime are not as different as one might expect.
Sources of this article
Aside from the standard textbooks (Misner, Thorne and Wheeler etc.) an important source of information for this article is the writing of scientists such as Michel Janssen , John Stachel , John Norton , Jürgen Renn , and others. More particularly, the articles that I studied are a blend of history and philosophy of physics. In writing these articles the authors' aim is to discuss the underlying concepts that have motivated physicists in exploring the avenues they have explored.
John Norton:
'What was Einstein's principle of Equivalence?' (PDF-document, 376 KB) John Norton discusses that the version of the Equivalence principle that is commonly offered in expositions of general relativity fundamentally differs in content from the principle that Einstein presented in his papers. Norton judges Einstein's version to be preferable. Download from pitt.edu
'General Covariance and the Foundations of General Relativity: Eight Decades of Dispute' (PDF-document, 460 KB) Download from pitt.edu
Documentation:
The expression 'inertio-gravitational field'
The expression 'inertio-gravitational field' has been introduced by John Stachel, in the 1990s. (John Stachel has confirmed to me that as far as he knows he introduced it.) In particular the authors John Stachel and Michel Janssen use it to clarify underlying concepts. The expression 'inertio-gravitational field' fits like a glove, and in due course I expect it to become a standard expression in the education of relativistic physics.
Timeline of publications by John Stachel.
- 1987: "the gravitational-cum-inertial field" in "How Einstein Discovered General Relativity: A Historical Tale with Some Contemporary Morals" in M.A. H. MacCallum, ed., General Relativity and Gravitation/ Proceedings of the 11th International Conference on General Relativity and Gravitation (Cambridge U. P. 1987), pp. 200-208. [Conference held in 1986]
- 1991: "the gravitational-cum-inertial field" on p. 32 of "Einstein and Quantum Mechanics" in John Stachel and Abhay Ashtekar, eds., Conceptual Problems of Quantum Gravity/Based on the Proceedings of the 1988 Osgood Hill Conference (Birkhäuser 1991), pp. 13-42.
- 1993: "the inertio-gravitational field" on p. 136 of "The Meaning of General Covariance: The Hole Story," in John Earman et al, eds., Philosophical Problems of the Internal and External World (University of Pittsburgh Press/Universitätsverlag Konstanz 1993), pp. 129-160.
- 1994: "the inertio-gravitational field" on p. 153 of "Changes in the Concepts of Space and Time Brought About by Relativity," in Carol Gould and Robert S. Cohen, eds, Artifacts, Representations and Social Practice (Kluwer Academic 1994) pp. 141-162.
List of publications that are available for download in which the expression 'Inertio-gravitational field' is used
- Structure, Individuality and Quantum Gravity (PDF-document, 333 KB) Download from arxiv.org
- The Hole Argument for Covariant Theories (PDF-document, 176 KB) Download from arxiv.org
- Einstein's first systematic exposition of general relativity (PDF-document, 187 KB) Michel Janssen discusses the concepts in Einstein's exposition.
Download from philsci-archive.pitt.edu
- Relativity (PDF-document, 88 KB) Article about relativity for the Dictionary of the History of Ideas Download from philsci-archive.pitt.edu
- The Einstein-Besso Manuscript: A Glimpse Behind the Curtain of the Wizard (PDF-document, 1.3 MB) Download from tc.umn.edu
- A Journey More Important Than Its Destination: Einstein's Quest for General Relativity,1907-1920. (PDF-document, 1.7 MB) A series of slides, with pictures and summary text to illustrate the development of ideas. Download from tc.umn.edu
- 'Lecture 4: General Covariance and gauge theories'(PDF-document, 107 KB) Download from users.ox.ac.uk
Dennis Lehmkuhl
- Why Einstein did not believe that General Relativity geometrizes gravity (PDF-document, 231 KB) Download from sciencedirect.com (no paywall) (also available for download from PhilSciArchive
Books in which the expression 'inertio-gravitational field' is used.
·Abhay Ashtekar 100 Years of Relativity: Space-time Structure : Einstein and Beyond
·Ignazio Ciufolini, Daniele Dominici, L. Lusanna , 2001: A Relativistic Spacetime Odyssey
·Andrew Warwick Masters of Theory: Cambridge and the Rise of Mathematical Physics

This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.
Last time this page was modified: March 17 2025