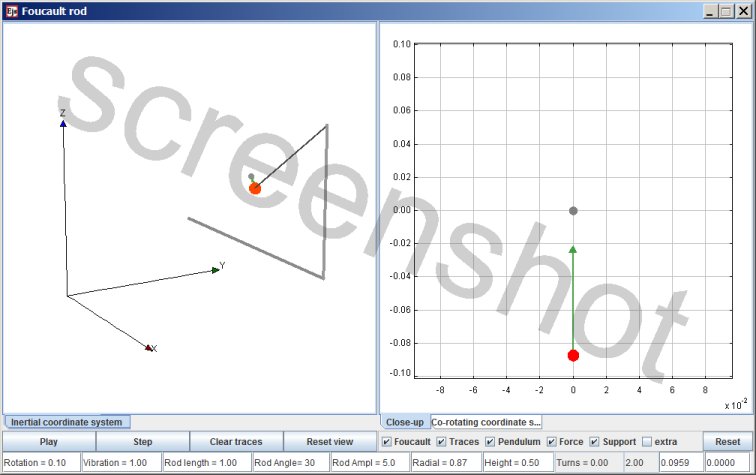
Foucault rod
This simulation models the following setup:
A rod with a weight at the end; the flexible rod is vibrating. The base of the rod is firmly secured to a support, the weight at the other end of the rod is like the bob of a pendulum. The support of the rod is rotating, so that the rod is circumnavigating a central axis. When the bob is released it starts to vibrate from co-rotating motion.
This simulation models the tabletop device that is on display in the Physics and Arts exhibition at the University at Buffalo, State University of New York.
- Slide show displaying the device
- Flash video showing an overall view
- Flash video showing a close-up view
In addition, in this simulation the angle of the rod and the distance of the pendulum bob to the central axis of rotation can be varied independently.
Displacement of the midpoint of the swing
When the system is rotating the midpoint of the swing is shifted outwards.
The restoring force from the elasticity of the rod can be thought of as decomposed in a component that provides required centripetal force, and a component that just sustains the vibration. When the pendulum bob is swinging from left to right it is alternating between circumnavigating the central axis slower than the overall rotation rate and circumnavigating the central axis faster than the overall rotation rate. Whenever the pendulum bob circumnavigates slower the centripetal force pulls the pendulum bob closer to the central axis of rotation.
Precession rate dependent on the angle
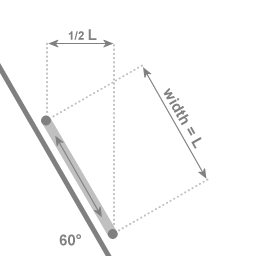
In the case of an angle of 60 degrees with the central axis of rotation: If the two extremal points of the swing are a distance of L apart, then the motion towards and away from the central axis covers a distance of 1/2 L
The precession rate is related to the amount of work that the centripetal force can do. When the pendulum bob moves closer to the central axis of rotation the centripetal force is doing work, when the pendulum bob moves away from the central axis of rotation the pendulum bob is doing negative work.
When the pendulum rod is oriented parallel to the central axis of rotation the plane of swing has its maximum precession. With the rod at an angle to the central axis of rotation the amount of work that the centripetal force can do is reduced, resulting in a correspondingly slower precession.
The input fields
- Rotation. System rotation rate; the angular velocity of the rod support.
- Vibration. How fast the rod vibrates.
- Rod length. With a very large value, such as 5, the swing will fill the entire display.
- Rod angle. Angle (degrees) of the rod relative to the horizontal plane. If you change the angle then the field next to the 'turns' field will change also, showing the expected period to complete a precession cycle.
- Rod Amplitude. The width of the swing.
- Radial. Radial distance (of the bob) to the central axis of rotation. When you input a negative value the rod will point outward instead of inward. When the radial distance is zero the midpoint of the swing falls on the central axis of rotation.
- Height.Height of the pendulum bob with respect to the equatorial plane.
- Zoom. The zoom for the close-up view is set automatically to give a good view. The zoom can be further adjusted with this input field.
- Zoom shift. For shifting the close-up view.
- checkbox 'Foucault'. When this is checked then entering a new value for Rod Angle will also update Radial distance and Height, so that the rod will point towards the origin.
Suggested settings to explore
The plane of swing also turns when the midpoint of the swing lies on the central axis of rotation:
Rod Length: 8
Rod amplitude: 15
Radial distance: 0
Height: 0
The Foucault turning is remarkably robust; with a huge amplitude the oscillation is not a harmonic oscillation, but the motion remains very close to Foucault turning:
Rod length : 1
Rod amplitude: 30
Method of computation
I discuss the mathematical setup of this Foucault rod simulation in a separate article: Foucault rod mathematics.
This simulation has been created with EJS
EJS stores the specifications of a simulation in a plain text file, with extension .xml
You can examine how the simulation has been set up by opening the simulation .xml file with EJS.
Download location for the EJS software
Download location for the Foucault rod source file
(The file is zipped because a browser will attempt to parse any .xml file.)

This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.
Last time this page was modified: June 18 2017