Conservation of angular momentum, second part
This article continues the discussion of angular momentum of circumnavigating objects that was started in the article Angular momentum of orbiting objects. Please read that article first.
Energy conversions and angular momentum
In the preceding article I discussed Newton's proof of conservation of angular momentum. In this article my purpose is to show that conservation of angular momentum can be derived by evaluating the work that is done when a rotating system contracts.
Deriving conservation of angular momentum from energy energy conversion is quite the cumbersome method; it's certainly not practical. The purpose of the following derivation is to prove a point. The conservation principles are interderivable, and conservation of angular momentum can be derived from other principles.
Additionally I've created a Java applet that illustrates the physics of angular acceleration due to contraction.
Elastic compression analogy
Take the case of cilinder filled with air, already pressurized, and that air is further compressed by a force exerted on the piston. The compressing force is doing work upon the air; the amount of work is proportional to the displacement of the piston. The compression of the gas in the cilinder increases the energy content. That increase of energy content gives additional rise of the pressure of the gas. Achieving further compresssion becomes harder and harder.
Two weights connected to pistons. Hydraulic machinery (not shown) pulls the weights closer to the center of rotation, causing angular acceleration.
To contract a rotating assembly requires doing work. The work done speeds up the assembly. At that larger angular velocity a larger centripetal force is required.
As shown in animation 1.: as the sytem contracts the radius of circumnavigation decreases, but because of the increase in angular velocity the higher energy state requires a larger centripetal force in order to sustain circular motion.
The concept of doing negative work
First I need to discuss the concept of doing negative work, using the case of compressing a gas as example.
When you are compressing a gas you are doing work upon the gas, and potential energy accumulates. As the gas is being compressed the outward pressure force is doing negative work. Doing negative work is the inverse of doing work.
Next: relax your effort to compress the gas, doing so gradually. As you let out the piston the gas reverts towards a less compressed state. Even though you are still exerting a force you allow the piston to move against the force you are exerting. That means: during the relaxation the force you are still exerting is doing negative work upon the gas.
Now: in the case of compressing a gas there is a pair of opposing forces: you compressing the gas, with the gas pressure acting in opposition to that. Whenever one of the pair is doing negative work the other is doing positive work, and consequently it's always possible account for the physics taking place in terms of positive work.
However, in the case of the rotating assembly we do need the concept of negative work. When you stop contracting a rotating assembly and allow it to expand again kinetic energy flows out of the rotating system. Since there is only one force - the centripetal force - the only way to account for the outflow of energy is in terms of the centripetal force doing negative work.
Moving down a ramp
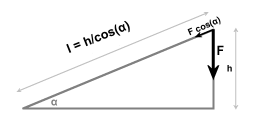
Sliding down a ramp or moving straight in the direction of the force results in the same amount of work done.
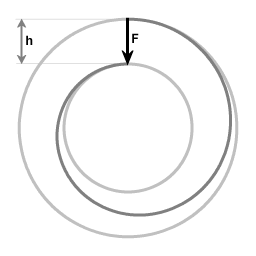
Moving along an inward spiral is like moving down a ramp.
Another analogy: moving along a spiral is like moving down a ramp.
Diagram 2 illustrates the case of moving down over a height h. The motion can be either straight down, parallel to the direction of the force, or the motion can be along a ramp. In both cases the final kinetic energy is the same. The presence of the ramp affects the direction of the final velocity, but for calculating the amount of work done you simply multiply the force F with height h.
Diagram 3 illustrates that an inward spiralling trajectory is like moving down a ramp. Initially the object is moving along the outer circle, then it's pulled closer to the center, settling on moving along the inner circle. It's not necessary to know the shape of the spiraling trajectory. The amount of work that is done is the force multiplied with the height difference h.
Infinitesimal case
I start with the simplified case where at all time the deviation from circular motion is small. That gives an approximation that is exact in the limit of infinitisimal deviation from circular motion. Following that I will discuss the derivation of the general case.
Let an object be in circular motion. At some point in time the centripetal force increases a small amount, and accordingly the object is drawn closer to the center of rotation. For a period of time the centripetal force is continuously adjusted upwardly, always a small amount stronger than necessary for sustaining circular motion at the instantaneous angular velocity and radial distance. Finally, the centripetal force is no longer adjusted upwardly, and the contraction ceases. If the radius of circular motion has been halved, how much has the angular velocity increased?
The kinetic energy of an object in circular motion is ½mr²ω², where r is the radius and ω is the angular velocity. At each distance r to the center of rotation the magnitude of the required centripetal force is mω²r . The change in kinetic energy equals the work that is being done. ΔE = F *Δr.
Of course, the expression ΔE = F *Δr is valid only for a case where the centripetal force is constant. In this case F is a function of ω and r, and to get a valid expression the differential form must be used: dE/dr = F.
![\begin{array}{lcl} F & = & -m \omega^2 r \\[3pt] E_k & = & \tfrac{1}{2}mr^2\omega^2 \\[2pt] \cfrac{dE_k}{dr} } & = & F \end{array}](../momentum_img/20230807_142000_442x306.png)
As a rotating system contracts the following four quantities are all four being changed around: kinetic energy, centripetal force, angular velocity and radial distance. The three relations that are laid out in (1) will allow us to narrow down to a relation between angular velocity and radial distance.
Substituting the expressions for E and F into the differential relation gives:
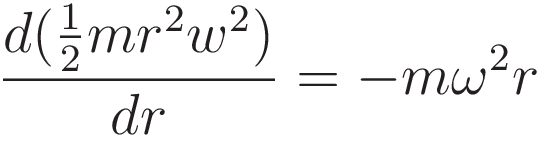
Make the following substitution:
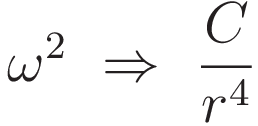
Where C is a constant.
(4) shows the verification: taking the derivative specified on the left hand side produces the right hand side:
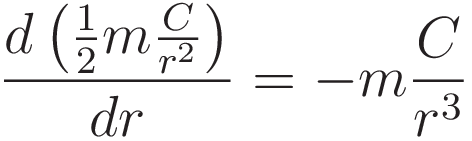
The expression ω2 = C/r4 rearranges to a squared version of the familiar expression for angular momentum conservation: ω2r4 = C.
The general case
In the general case at each point in time the centripetal force can be larger, equal to or smaller than the amount of force that is required for sustaining circular motion. A general treatment accomodates that explicitly.
At this point it is helpful to proceed with decomposition of the total kinetic energy into two perpendicular components: instantaneous kinetic energy of motion in radial direction, and instantaneous angular kinetic energy.
The expression for the total kinetic energy, decomposed in radial component and angular component:

The amount of centripetal force that is available for radial acceleration is the total force minus the required centripetal force.
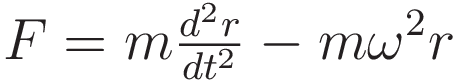
Substituting the expressions above into the differential relation dE/dr = F gives the following:
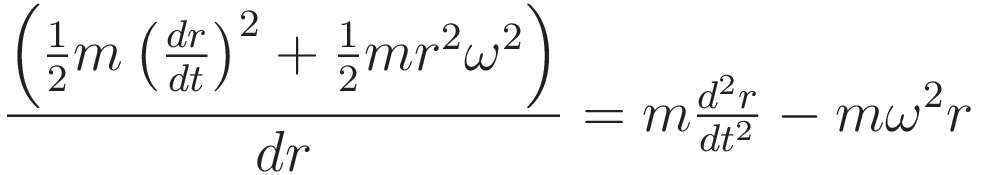
The above equation can be seen as a combination of two equations: (8a) and (8b):


We verify that the left hand side and the right hand side of (8a) are the same:
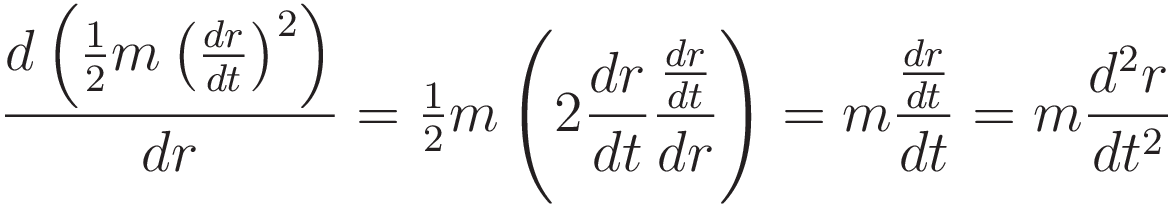
The left hand side and the right side of (8a) are the same; it follows: no matter what the instantaneous radial acceleration is, inward or outward, at all times the motion will satisfy the relation (8b). (8b) is the same as (2), demonstrating that when a centripetal force is doing work the amount of work done enforces conservation of angular momentum.
It is of course not the case that the relations (8a) and (8b) are independent relations.
Radial velocity is an intermediary in this case. The immediate effect of an increase of centripetal force is that the circumnavigating object acquires a radial velocity. A quarter of a turn later that radial velocity has shifted to circumnavigating velocity.
Cause and effect
This particular derivation is along lines of cause-and-effect: when a centripetal force is doing work, it causes angular acceleration. The amount of angular acceleration is such that a quantity proportional to ωr² is conserved.
Like all derivations of conservation of angular momentum, this derivation rests on a symmetry. The notation is in polar coordinates: points in space are denoted with a radial distance r and an angle θ. The magnitude of the centripetal force is not a function of the angle θ, hence the angle θ does not even enter the derivation.

This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.
Last time this page was modified: August 08 2023