Conservation of angular momentum
Introduction
Two weights connected to pistons. Hydraulic machinery (not shown) pulls the weights closer to the center of rotation, causing angular acceleration.
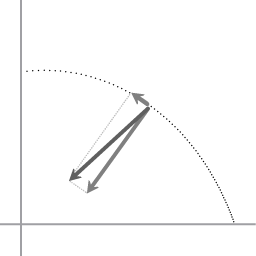
Typical trajectory during contraction. The centripetal force can be decomposed in a perpendicular and an tangential component.
The general scope of angular momentum covers phenomena that may seem hardly related:
- The angular momentum that is involved in circumnavigating motion, such as planetary orbits
- The angular momentum of a spinning solid.
The common factor is that angular momentum involves two or more objects that are exerting a force on each other so they don't fly apart.
A solid object can be thought of as all of it's constituent atoms, with the bonding strength of the material providing the required force. If a object spins faster than the bonding strength can handle the object tears apart.
In this article I focus on the case where the motion is circumnavigating, and with the attractive force strong enough to even contract the system.
Contraction of a rotating system
Animation 1 depicts that when a rotating assembly contracts the angular velocity increases. Inversely, when the distance to the center of rotation increases the angular velocity goes down.
Image 2 plots the motion of one of the spheres as the assembly contracts. In the diagram the darkest arrow represents the centripetal force. The origin of the coordinate system has been positioned at the center point of the rotation.
Decomposition
To visualise the effect of the contracting force it is helpful to think of it as decomposed into two components that are perpendicular to each other: one component perpendicular to the instantaneous velocity, the other tangent to the instantaneous velocity. The perpendicular component causes change of direction; the tangent component causes change of speed. That is, the force that contracts the rotating system will speed it up.
How much?
What we would like to know is how much angular acceleration there will be because of the contraction. In the history of physics this problem was very important. Its solution, first found for celestial mechanics, was a breakthrough development.
History
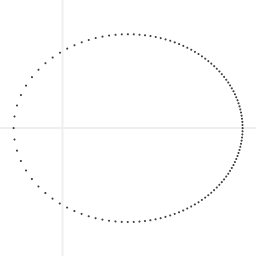
A Kepler orbit with a large eccentricity. The dots are spaced in equal time intervals.
Kepler had hypothesized that the shape of a planetary orbit is an ellipse (with the Sun at one focus), but that was not enough to have a theory of celestial motion; he also needed a rule that describes how the velocity changes over time.
As is well known: Kepler discovered a law of areas: as planets circumnavigate the Sun: in equal amounts of time equal areas are swept out. For Kepler his area law was an empirical law; he had no way of knowing whether it was a separate law or an integral part of some larger theory of motion. Newton showed the latter was the case.
The very first theorem in Newton's Principia is the area law. In fact, Newton derived a more general form of the area law, showing that it applies not only for the Sun's gravity, but for any central force. I will call this generalized form 'Newton's law of areas'.
Derivation of the area law
I will first present Newtons derivation, and then I will show how Newton's area law and the modern concept of conservation of angular momentum are equivalent.
Elements
Newton's derivation relies on the following elements:
- The principle of conservation of linear velocity (Newton's first law).
- The rules of composition of velocity.
- Conservation of momentum when two objects exert a force upon each other.
- No dependency on orientation (rotational symmetry).
The fourth element of this list, rotational symmetry, is unique to angular momentum; it is a defining characteristic. The gravitational force exerted by the Sun is acts in radial direction, hence rotational symmetry.
Reasoning

Two objects, R and T, moving with constant momentum. Hence the momentum of the common center of mass, S, is constant.
The area law in the case of uniform velocity.
The law of conservation of linear velocity asserts a principle of proportion:
- If no force is exerted on an object (or if the forces cancel out) then in equal intervals of time the object will cover equal distances.
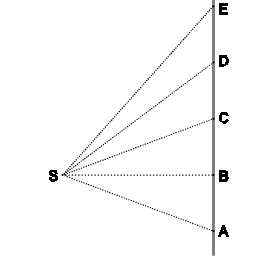
In image 5 the thick line depicts the law of conservation of linear velocity. An object moves along the points A, B, C, D, E, covering equal distances in equal intervals of time. It is convenient to take as point S the common center of mass of two objects, R and T (as shown in image 4). The dotted lines mark triangles. Clearly SAB, SBC, SCD and SDE all have the same area: equal areas are swept out in equal intervals of time. This shows how conservation of linear velocity and the area law are interconnected. When no force acts conservation of linear velocity and the area law are one and the same principle.
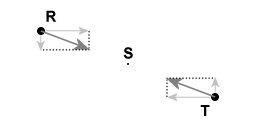
The objects R and T exert a force on each other. The momentum of their common center of mass is conserved.
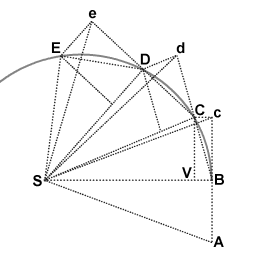
Geometric demonstration of the area law following from the laws of motion.
Image 6 emphasizes a property of point S, the common center of two objects: when object R and object T exert a force on each other the momentum of the common center of mass is conserved.
Image 7 shows Newton's geometric demonstration of the law of areas. The diagram is a slightly modified version of the diagram that Newton gave in the Principia; the mathematics is the same.
Object T (not shown in image 7) is moving along the curvilinear trajectory that goes through the points A, B, C, D and E. The force experienced by object T causes change of velocity. For the derivation the continuous change of velocity is approximated with instantaneous changes of velocity that occur at equal intervals of time. In the limit of ever smaller intervals of time the sequence of the instantaneous changes of velocity approaches infinitely close to a continuous change of velocity.
Point S is the common center of mass of the objects R and T. Objects R and T exert a distance dependent force upon each other. The force that objects R and T exert upon each other is mutual: that ensures that the state of motion of point S is inertial motion. For the proof it suffices that point S is in a state of inertial motion and that the force that is exerted upon object T is directed towards point S at all times.
At point B, object T receives an impulse towards point S, resulting in a velocity component towards point S. Had object T not received that impulse, it would have proceeded to point c (in an equal amount of time).
The actual displacement BC is the vector sum of the displacements Bc and BV. The triangles SAB and SBc have the same area. Since the lines SB and Cc are parallel, the triangles SBc and SBC have the same area. Hence, the triangles SAB and SBC have the same area.
The points B, C and d are on the same line. If object T would not receive an impulse at point C then in an equal amount of time it would proceed to point d. Since the laws of motion are the same for any orientation in space the same reasoning can be repeated for the subsequent triangles, thus demonstrating that the triangles SBC, SCD and SDE that are swept out in equal intervals of time, have equal area.
In the limit of ever smaller intervals of time, the line sections BC, CD and DE approach ever closer to the curvilinear trajectory.
Angular momentum
The next step is to find an an algebraic expression for Newton's law of areas, so that the principle can be put to use in calculations.
The surface area of a triangle is proportional to the product of the base and the height. Here the base of each triangle is r, the radial distance, and the height is r·Δθ (where Δθ is the angle that is swept out during the time interval Δt)
Dividing the area by the interval of time gives the amount of area that is swept out per unit of time.
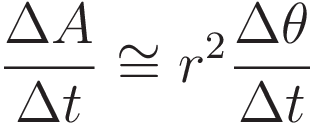
In the limit of Δt going to infinitisimal the expression for the conserved quantity is proportional to the following expression:
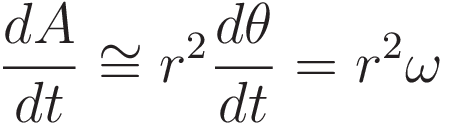
Where ω is the angular velocity.
So we have the following conserved quantity: r2ω
Radial distance and angular velocity
The area law expresses a relation between radial distance and angular velocity.
At the beginning I raised the question: when the rotating assembly contracts, how much angular acceleration will the contraction cause? The answer to that question is the relation: r2ω.
The relation is quadratic in 'r', which means you get a lot of angular acceleration. For instance: when the radial distance has been halved the angular velocity will have been quadrupled.
Angular momentum
The relation r2ω forms the basis of the concept of angular momentum.
Angular momentum L is defined as the product of the moment of inertia and angular velocity. L = mr²ω. The convenience of defining angular momentum that way is that it slots in with kinetic energy. The kinetic energy of an object that follows a circular trajectory is ½mv². We can make the following substitution: v = ωr, which gives an expression for the kinetic energy associated with circular motion: ½mr²ω²
The quantiy mr² is called the 'moment of inertia' and it is the rotational counterpart of inertia.
Causality

Repeat of animation 1. Two weights connected to pistons. Hydraulic machinery (not shown) pulls the weights closer to the center of rotation, causing angular acceleration.
Momentum deals with spatial symmetry of the laws of physics, rather than with a cause-to-effect relation. This can be shown with the example of a cannon being fired. When a cannon is fired, the projectile will shoot out of the barrel towards the target, and the barrel will recoil. It would be wrong to suggest that the projectile leaves the barrel at high velocity because of the recoil of the barrel. The projectile being fired and the recoil of the barrel occur simultaneously, hence either one cannot be the cause of the other.
The causal mechanism is in the preceding energy conversions: the explosion of the gun powder converts potential chemical energy to the potential energy of a highly compressed gas. As the gas expands, its high pressure exerts a force on both the projectile and the interior of the barrel. It is through the action of that force that potential energy is converted to kinetic energy of both projectile and barrel.
Similarly, in the case of angular acceleration due to contraction of a rotating system, the increase of angular velocity on contraction is consistent with the principle of conservation of angular momentum, but that should not be confused with conservation of angular momentum being a causal agent. The causal agent is the centripetal force doing work.

This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.
Last time this page was modified: December 29 2023