
Source of the cartoon: XKCD webcomic
Centrifugal force
Centrifugal force is where gut feeling and formal reasoning appear to clash. In this article I intend to address on one side the way that gut feeling goes awry, and on the other side I want to explain why the formal reasoning proceeds in the way it does.
There is actually a James Bond film in which a villain's henchman attempts to kill Mr. Bond by cranking up the speed of a human centrifuge.
Movie physics aside, it's clear that it's possible to kill someone that way. Even carelessness could get someone killed. When the person in the human centrifuge loses consciousness the operators ease off immediately. If they wouldn't do that the brain would remain starved of blood and the astronaut/pilot would quickly die.
From cause to effect: gravitation
I'm using a sphere to illustrate the concepts because of its symmetry. With a sphere a force acting upon the sphere as a whole is naturally represented with a vector originating at the sphere's center.
In the case of the Earth's gravity one can think of three steps.

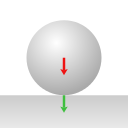
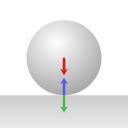
1. The Earth exerts a gravitational force upon all objects; the Earth exerts a gravitational force upon the sphere.
2. As a consequence, the sphere exerts a force upon the floor.
3. As a consequence, the floor exerts a force upon the sphere.
For each arrow the base of the arrow is positioned at the point where the force is exerted. The red arrow for gravity is positioned at the sphere's center, to represent that in calculations we can treat gravity as acting upon the center of mass.
Physical sensation

The image represents a stack of weighing scales. The topmost scale is not carrying weight, so the dial is all the way to the left at the zero position. As you look down the stack you see each scale indicating a higher weight; the weight of the stack of scales above it.
This represents your physical sensation when you are standing up. The soles of your feet are compressed the most, whereas your head is the least subject to that compression.
More generally, the image illustrates that whenever you measure gravity, you're not measuring it directly. What the weighing scale indicates is how much it is compressed. What is measured is that compression.
I want to take some more time to emphasize this: there is no such thing as measuring gravity directly. What is measured is something that arises from gravity: a compression because gravity acts on the body as a whole, whereas the floor that you are standing on acts upon the soles of your feet.
That is the physical experience, and the mind automatically translates that to sensing a gravitational force.
Centripetal acceleration

The image shows a rendering of the wheel shaped space station in the movie 2001: a space odessey.
The space station is rotating; weight is created by pulling G's.
From cause to effect: centripetal acceleration
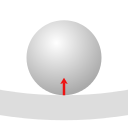
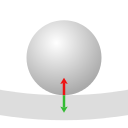
In the case of pulling G's the formal reasoning is as follows.
1. The floor exerts a force upon the sphere, maintaining a state of centripetal acceleration.
2. At the point of contact with the floor the sphere exerts an outward force upon the floor
In this case the formal reasoning has only two steps, and compared to the case of gravity the rundown of from cause to effect is the other way round. Between the case of gravitation and centripetal acceleration there is a reversal of what is identified as cause and what is identified as effect.
Identical sensation
In the case of gravitation and in the case of being subject to centripetal acceleration the physical sensation is identical, and you can't stop your mind from automatically translating the experience of compression to sensing a gravitational force. When you are in a state of centripetal acceleration your mind automatically supposes a centrifugal force. Specifically: a gravitational force in centrifugal direction that is being exerted upon you.
Inertia
There is inertia in the sense of Newton's first law and inertia in the sense of Newton's second law. Authors using the expression 'centrifugal force' sometimes have the first sense in mind, and sometimes the second, and often they shift from one sense to the other without announcing it, which I think they should.
If you are in a pilot training centrifuge, and you drop an object it will proceed to the floor and then hit the floor. Proceeding to the floor is described by Newton's first law: an object on which no force is exerted will move in a straight line. The pod of the pilot training centrifuge moves along a curvilinear path, and thus it intercepts the released object.
If you are in the pod of a pilot training centrifuge, and you are standing on a weighing scale, then inertia in the sense of Newton's second law is at play: a force is required to accelerate you, and the amount of force is proportional to your mass, hence the centrifugal force that you automatically suppose is proportional to your mass.
Formal reasoning
In formal physics reasoning, it's not allowed to refer to inertia as a force. In physics the concept of 'force' is defined as 'a reciprocal interaction between two objects'. Example: electrostatic interaction. Two electrically charged particles, one positive one negative, are in interaction with each other, giving rise to a mutual attractive force. It is very useful to keep the concept of force limited to reciprocal interactions only. Defining force in this way makes it slot in with Newton's third law. (Arguably, Newton's third law provides the very definition of what a force is.)
Inertia involves a single object; it does not have the characteristic of mutualness that typifies a force. It's best to assign inertia to a category of its own.
Putting reversal of cause and effect to use
There are circumstances where it can be useful to opt for thinking with reversed cause and effect. For instance, when you are thinking about the tension in helicopter blades during fast rotation. Then you visualize yourself as co-moving with the helicopter blades, and then you can imagine yourself experiencing a centrifugal force.
It's important, though, to keep thinking in terms of reversed cause and effect in its proper context. For example the case of the pilot training centrifuge. Let's say you are in the control room, and you're watching the machine go around. That is the inertial point of view, and it would be a big mistake to introduce the same reversed cause and effect into the motion with respect to the inertial point of view.
If you are drawing up a diagram that represents a snapshot in time of a system that is rotating, then you have to decide in advance whether you want it to represent an inertial point of view or a co-rotating point of view. Depending on your point of view you are assuming a different rundown from cause to effect.
I often notice a mixup. Some phenomenon is first discussed as seen from a co-rotating point of view, then the author announces a description as seen from an inertial point of view, but he keeps using the centrifugal force that applies only in the context of the co-rotating point of view.
The statement: "centrifugal force only exists in a rotating frame of reference" is another way of saying: "You can reverse cause and effect only in the context of a rotating frame of reference."

This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.
Last time this page was modified: June 18 2017