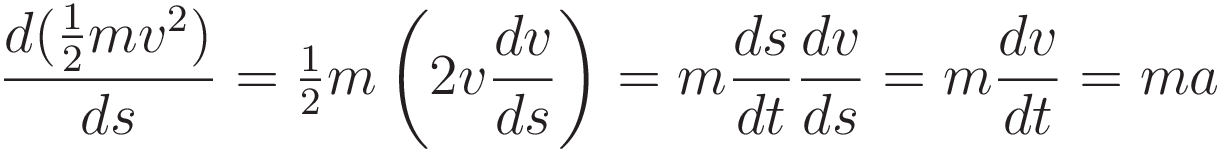The Euler-Lagrange equation in Dynamics
This article continues the exposition presented in the Energy-Position equation article.
My recommendation is to first absorb the content of that article; that content is the foundation of the information presented here.
The mathematical feature that underlies derivation of the Euler-Lagrange equation is expressed by a lemma that was first stated by Jacob Bernoulli.
When Johann Bernoulli had presented the Brachistochrone problem to the mathematicians of the time Jacob Bernoulli was among the few who solved it. The treatment by Jacob Bernoulli is in the Acta Eruditorum, May 1697, pp. 211-217
Jacob opens his treatment with an observation concerning the fact that the curve that is sought is a minimum.
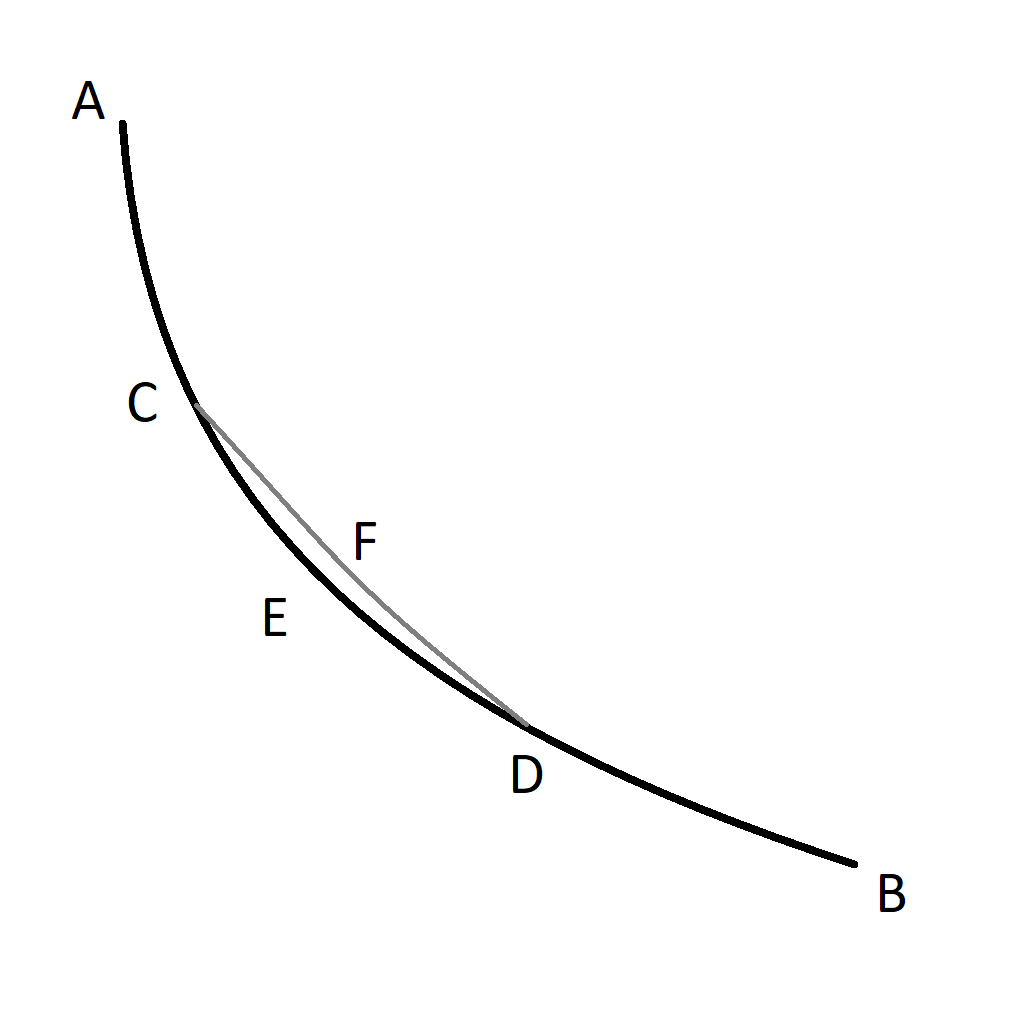
Jacob's Lemma
Lemma. Let ACEDB be the desired curve along which a heavy point falls from A to B in the shortest time, and let C and D be two points on it as close together as we like. Then the segment of arc CED is among all segments of arc with C and D as end points the segment that a heavy point falling from A traverses in the shortest time. Indeed, if another segment of arc CFD were traversed in a shorter time, then the point would move along ACFDB in a shorter time than along ACEDB, which is contrary to our supposition.
Jacob's lemma generalizes to all cases where the curve that you want to find is an extremum; either a maximum or a minimum. If the evaluation is an extremum for the entire curve, then it is also an extremum for any sub-section of the curve, down to infinitisimally short subsections.
The explicit statement of the brachistochrone problem is in terms of a global property: the amount of time it takes for an object to slide down the curve; it's in the form of evaluating an integral.
Jacob's lemma tells us: a restatement of the problem in the form of a differential equation must exist.
Variational calculus is the systematic way of capitalizing on the content of Jacob's lemma. The general Euler-Lagrange equation takes any problem stated in terms of variational calculus, and transforms the statement into a differential equation.
Class of trial trajectories
Graphlet 2 shows how the trajectory is varied, generating a class of trial trajectories. (The circle in the bottom section is the "knob" of a slider.) The startpoint and endpoint are fixed, in between the trajectory is varied. The set of all possible variations of the trajectory is much larger than this particular class of course, but for the purpose of this demonstration this simplest case is sufficient.
A start point and and end point are defined; the variation is constrained to be zero at the start point and end point.
From differential form to integral form
Dynamics taking place is evaluated by formulating and solving differential equations.
Variational calculus evaluates statements in integral form. The following section presents a demonstration that the differential equation can be restated in a form that involves an integral.
The starting point is the work-energy theorem:
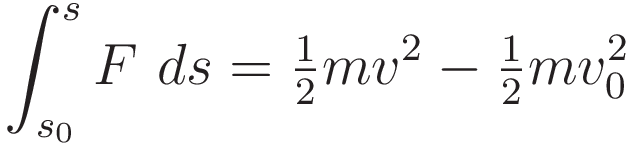
The work-energy theorem is only one step away from F=ma; the Work-Energy theorem is derived from F=ma by evaluating the integral of F=ma over distance. Hence taking the derivative with respect to position recovers F=ma.
Simplify to initial position coordinate zero and initial velocity zero.
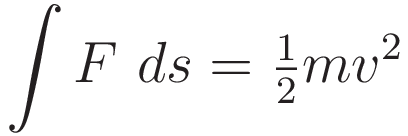
the derivative with respect to position:
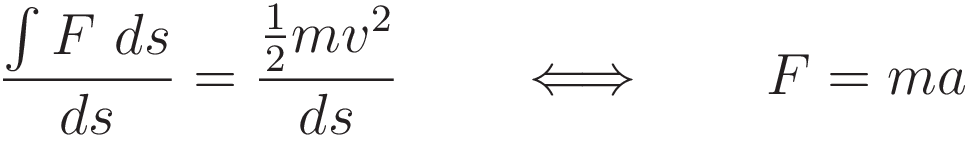
From here on I will refer to the negative of the integral of force over distance as the 'potential energy'.
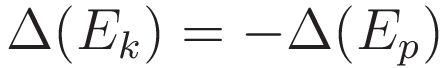
For the subsequent manipulations it is practical to move the minus sign inside the parentheses.

The validity of (1.5) extends down to infinitisimal change:
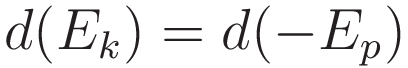
(1.6) is turned into a differential equation by taking the derivative with respect to position:

From here on I will refer to (1.7) as the 'Energy-Position equation', as it evaluates the derivative with respect to position.
We have the following property of integration: it is a linear operation:
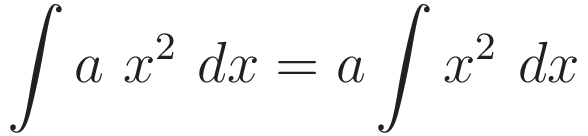
Therefore the value of the derivative of the energy propagates to the value of the derivative of the integral-of-the-energy.
For variation between two fixed points:
If, from start point to end point:

Then, from start point to end point:
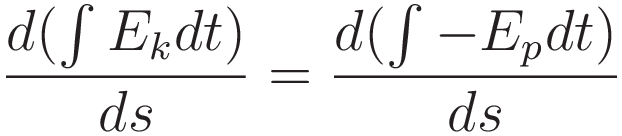
(1.8) is the foundation of the Hamilton's action. Hamilton's action is commonly notated with the letter 'S'. For the Energy I will use the letter 'E', with subscript; 'k' for 'kinetic' and 'p' for 'potential'
The way to capitalize on (1.8) in the the context of variational calculus is as follows:
In dynamics the variation is variation of position. In the process of sweeping out variation: when the trial trajectory coincides with the true trajectory the derivatives of the respective energies are changing at the same rate. It follows that when the trial trajectory coincides with the true trajectory the derivative of the action S will be zero.
Hamilton's action:
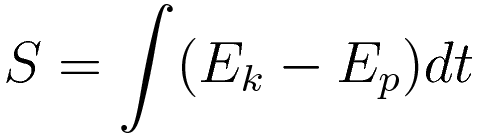
The EL-equation for dynamics
In the previous section 'from differential to integral form' it was demonstrated that the dynamics can be stated in a form that involves an integral.
In this section the treatment proceeds in the opposite direction. In this section the starting point is Hamilton's stationary action, and it is demonstrated that working back to a differential equation recovers F=ma, just as (1.3) shows that differentiating the work-energy theorem with respect to the spatial coordinate recovers F=ma.
(This demonstration is modeled after the demonstration in the discussion of Hamilton's stationary action in the Feynman Lectures. Details have been modified; the structure is copied.)
This demonstration is taylored for the context of classical mechanics. For one thing: for time, position and velocity the usual letters 't', 's' and 'v' are used.
(In the general case the functional may include one or more terms with a product of y(x) and and dy/dx, therefore in the general case a derivation must allow for that by specifying partial derivatives. (2.1) states the Lagrangian explicitly in terms of expressions for the respective energies, hence no need for specifying partial derivative.)
Hamilton's stationary action
Recapitulating Hamilton's stationary action:
When the trial trajectory coincides with the true trajectory the derivative of the action with respect to variation is zero.
Lagrangian
As we know, the Lagrangian 'L' is the sum of kinetic energy and minus potential energy. Here 'V(s)' stands for the potential as a function of the position coordinate 's'.

The kinetic energy is purely a function of ds/dt, and the potential energy V(s) is purely a function of the position coordinate 's'.
Hamilton's action:
![S=\int\biggl[\tfrac{1}{2}m\left(\frac{ds}{dt}\right)^2-V(s)\biggr]dt](../action_img/20210605_202800_758x156.png)
In (2.2) the position 's' is indicated with just the symbol 's'. But of course the trajectory is as yet undetermined, so here 's' represents the class of all trajectories that connect the start point and end point.
The variation is expressed with the symbol η. The underline indicates that the variation is with respect to the value for the spatial coordinate s of a particular trajectory among the class of all candidate trajectories.
![\int_{t_1}^{t_2}\biggl[\tfrac{1}{2}m\left(\frac{d\underline{s}}{dt}+\frac{d\eta}{dt}\right)^2-V(\underline{s}+\eta)\biggr]dt](../action_img/20210605_204600_924x160.png)
Multiplying out the expression for the kinetic energy term:
(the term with dη that is quadratic will later be dropped.)
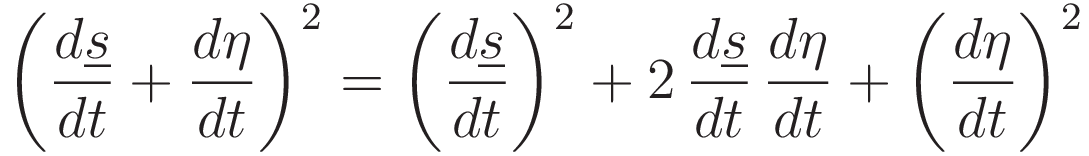
Since this derivation is intended for the general case we must allow the potential to be any function that can arise from integrating any physical force.
To accommodate the general case: for the potential energy a Taylor series expansion is applied:
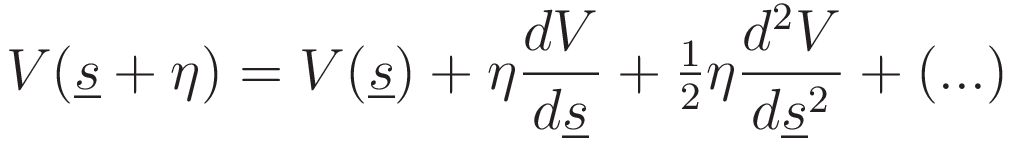
The following expression gives the action plus the variation of the action, with terms quadratic and higher dropped:
![S + \delta S = \int_{t_1}^{t_2}\biggl[\tfrac{1}{2}m\left(\frac{d\underline{s}}{dt}\right)^2+m\,\frac{d\underline{s}}{dt}\,\frac{d\eta}{dt} -V(\underline{s}) - \eta \frac{dV}{d\underline{s}}}\biggr]dt](../action_img/20210606_064100_1400x160.png)
Narrowing down to just the variation:
![\delta S = \int_{t_1}^{t_2}\biggl[m\,\frac{d\underline{s}}{dt}\,\frac{d\eta}{dt} - \eta \frac{dV}{d\underline{s}}\biggr]dt](../action_img/20210606_083800_768x156.png)
In reaching (2.7) a lot has already been accomplished.
(2.7) takes the derivative of the potential energy 'V' with respect to the spatial coordinate. This is because the variation is variation of the spatial coordinate. Taking the derivative of the potential energy with respect to the spatial coordinate first appeared in (2.5), and that was immediately the final form of the expression for the potential energy; this form carries through to (2.12).
Kinetic energy is proportional to the square of the velocity, which gives a term with the variation squared. (2.7) no longer has a squaring operation; the squaring operation has been replaced with taking the derivative of the variation with respect to time.
In order to make progress this derivative of the variation with respect to time must be transformed to an expression that is not a derivative of the variation, but the variation itself. The standard way to achieve this is by using integration by parts.
Integration by parts
The product rule of differentiation:
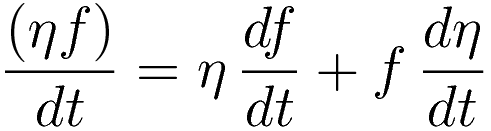
Rearranging:
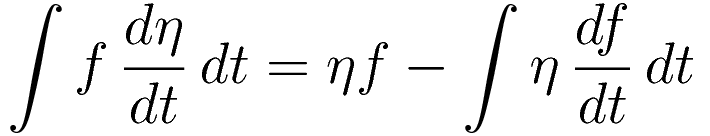
The term  in (2.7) corresponds to the 'f' in (2.9). That is the substitution that is performed to arrive at the following:
in (2.7) corresponds to the 'f' in (2.9). That is the substitution that is performed to arrive at the following:
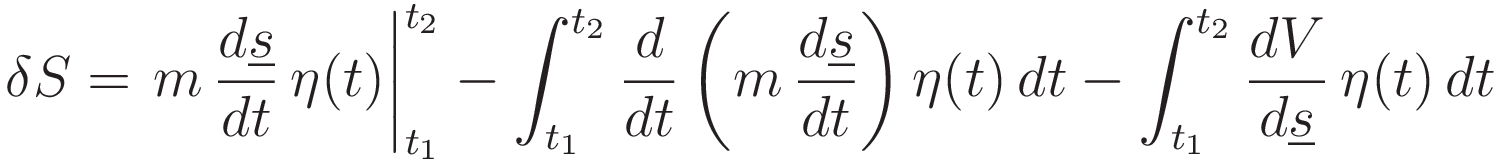
The variation is constrained to have the following properties: η(t1) = 0 and η(t2) = 0, hence the first term on the right hand side is zero.
Collecting the terms and rearranging:
![\delta S=\int_{t_1}^{t_2}\biggl[
-m\,\frac{d^2\underline{s}}{dt^2}-\frac{dV}{d\underline{s}}
\biggr]\eta(t)\,dt](../action_img/20210606_133000_826x156.png)
Now the equation has arrived at a form with only the variation itself (no derivative of it). This is what allows us to write an equation that when solved will give the true trajectory.
We are looking for the point where the derivative of Hamilton's action is zero, hence the point where δS is zero. The function η(t) is not zero, hence (2.11) is satisfied if and only if the part inside the square brackets is zero the entire time.
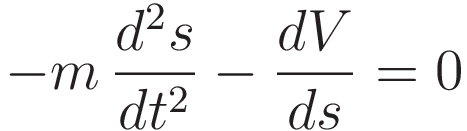
The term with the factor m has been transformed to a second derivative; the second derivative of position with respect to time: acceleration. The second term of (2.12), for the potential energy, was already established all the way back in (2.6); the derivative of the potential with respect to position: the force.
This completes the verification that if you work your way back from the integral form (1.8) to the differential form you end up recovering F=ma.
The Euler-Lagrange equation
In dynamics the result of deriving the Euler-Lagrange equation is that the Energy-Position equation (1.7) is recovered
The full EL-equation with the Lagrangian:
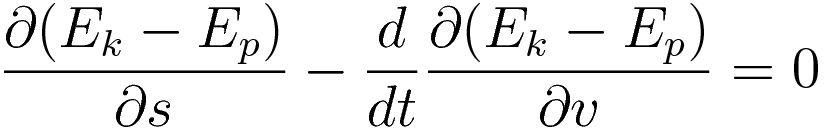
For the purpose of this comparison the Lagrangian-in-EL-equation simplifies to the following form:
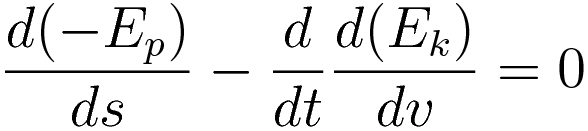
The term with the potential energy is already identical to the one in the Energy-Position equation (1.7).
Evaluating the term with kinetic energy:
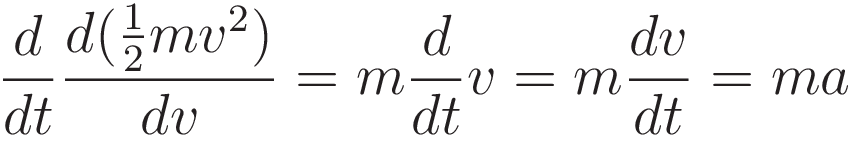
(1.7) and (3.2) evaluate to the same expression. This completes the verification that the Lagrangian-in-EulerLagrange-equation (3.1) is identical to the Energy-Position equation (1.7)
Discussion
Of course, this raises the question: what is the purpose of deriving an equation that you already know?
One consideration is this: while in dynamics the differential equation is already known that is not in general the case.
The problem that is seen as the origin of Calculus of variations is the Brachistochrone problem. While the Brachistochrone problem involves dynamics, it is not a dynamics problem.
When the Euler-Lagrange equation is used to solve the Brachistochrone problem the quantity for which an extremum is to be found is the time it takes from start point to end point. On the other hand: in dynamics the sought after trajectory is identified by inserting the Lagrangian Ek - Ep in the Euler-Lagrange equation. That difference arises from the fact that the Brachistochrone problem is not a dynamics problem.
For better or for worse: in physics textbooks the standard practice is to derive the general purpose Euler-Lagrange equation so that solving the Brachistochrone problem is supported too.
Derivation of the Work-Energy theorem
The steps in the following derivation are all towards the end goal of obtaining an expression in terms of the velocity v. In the course of the derivation the following two relations will be used:
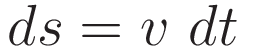
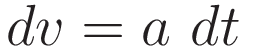
The integral for acceleration from a starting point s0 to a final point s
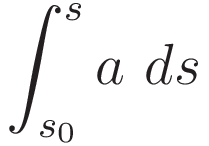
Intermediary step: change of the differential according to (4.1), with corresponding change of limits.
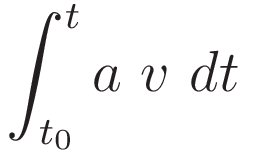
Change the order:
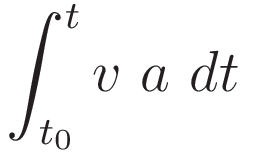
Change of the differential according to (4.2), with corresponding change of limits.
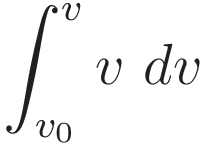
So we have:
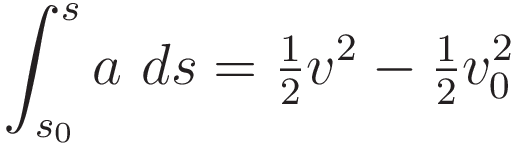
Up to this point no physics has been stated. (4.7) follows from the definitions of velocity and acceleration, combined with the mathematical properties of differentiation/integration.
Multiplying both sides with m and combining with F = ma arrives at a physics statement: the Work-Energy theorem:
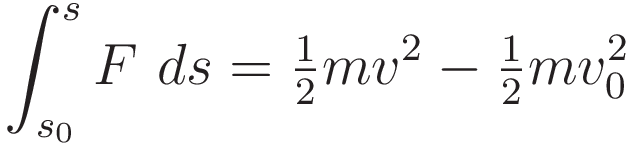
The interactive animations on this page were created with the Javascript Library JSXGraph. JSXGraph is developed at the Lehrstuhl für Mathematik und ihre Didaktik, University of Bayreuth, Germany.

This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.
Last time this page was modified: July 27 2021